How to find the value of the argument at a given value of the function

The function can be specified as mathematical expressions or graphical image. If the polynomial written in canonical form, and the schedule is recognizable curve, it is possible to determine the value of the argument in different parts of the coordinate plane. For example, if you specify a function Y=√x, then the argument can take only positive values. And for the function F=1/x is unacceptable the value of the argument x=0.

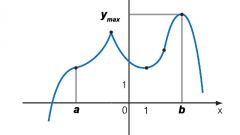
If the function is specified graphically some arbitrary curve, conclusions about the values of the argument can be done only on the visible part of graphics in the coordinate space. It is possible that different intervals have different functional dependencies. To find the value of the argument corresponding to a particular value of the function, find the specified number to the axis OY. From this point, draw a perpendicular to the intersection with the given curve. From the resulting point drop a perpendicular on the axis OX. The number on the x-axis is the required value of the argument. It is possible that the perpendicular y-axis crosses at several points. In this case from each point of intersection drop perpendiculars to the x-axis and record was found numeric values of the argument. They all match the specified numeric value to the function.

If the function is specified by a mathematical expression, first simplify the entry. Then to find the argument to solve the equation, equating a mathematical expression for a given value of the function. For example, for the function Y=x2 the value of the function Y=4 correspond to the value of the argument h=2 and h=-2. These values are obtained from the solution of the equation x2 =4.