How to find the maximum point of the function

The process of finding a local extremum is called the study of the function and is done by examining the first and second derivative of the function. Before the start of the study verify that the interval parameter value belongs to the valid values. For example, for the function F=1/x the value of the argument x=0 is not allowed. Or for a function Y=tg(x) argument cannot have a value of x=90°.

Verify that the function Y is differentiable for all specified interval. Find the first derivative Y'. It is obvious that before reaching the points of local maximum, the function increases, and the transition through the maximum, the function becomes decreasing. The first derivative in its physical sense a measure of the rate of change of a function. While the function increases, the speed of this process is a positive value. When passing through the local maximum of the function begins to decrease, and the rate of changing the function becomes negative. The transition rate of change of the function through zero occurs at the point of local maximum.

Therefore, on a plot of increase of the function, its first derivative is positive for all values of the argument in this interval. And Vice versa — on a plot of decreasing function value of the first derivative is less than zero. At the point of local maximum value of the first derivative is zero. Obviously, to find the local maximum of the function, it is necessary to find a point h in which the first derivative of this function equal to zero. If any argument value for the observable part x<h derivative must be positive, and for x>h - negative.

To find x solve the equation Y'=0. The value of Y(h) is a local maximum if the second derivative of the function at this point is less than zero. Find the second derivative Y", substitute in the obtained expression the value of the argument x= h and compare the result with zero.

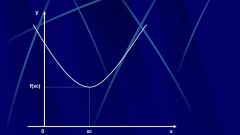
For example, the function Y=-x2+x+1 over the interval from -1 to 1 has continuous derivative Y'=-2x+1. When x=1/2 the derivative is equal to zero, and the transition through this point the derivative changes sign from "+" to "-". The second derivative Y"=-2. Build on the points of the graph of the function Y=-x2+x+1 and check whether the point with abscissa x=1/2 a local maximum at a specified numeric interval axis.