Instruction
1
A function y = F(x) is increasing on a particular interval if for any points x1 < x2 on this interval the condition F(x1) < F(x2). I.e. the greater the argument value, the greater the value of the function. For a decreasing function true F(x1) > F(x2), where x1 > x2 for any point on the interval.
2
There are sufficient signs of ascending & descending functions, which are derived from the result of calculating the derivative. If the derivative of the function is positive for any point of the interval, the function is increasing, if negative, decreases.
3
To find the intervals of increase and decrease functions, you need to find the area of its definition, calculate the derivative, solve the inequality F’(x) > 0 and F’(x) < 0, and then included in the resulting interval boundary points at which the function is continuous and defined to exclude those in which its value cannot be determined.
4
Let's consider an example.
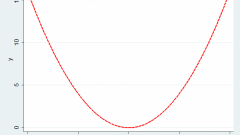
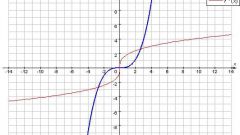
Find the intervals of increasing and decreasing function for y = (3·x2 + 2·x - 4)/x2.
5
Solution.
1. Find the domain of the function. Clearly, the expression standing in the denominator should always be different from zero. Therefore, the point 0 is excluded from the scope: the function is defined at x ∈ (-∞; 0)∪(0; +∞).
6
2. Compute the derivative of the function:
y’(x) = ((3·x2 + 2·x - 4)’ ·x2 – (3·x2 + 2·x - 4) · (x2)’)/x^4 = ((6·x + 2) ·x2 – (3·x2 + 2·x - 4) ·2·x)/x^4 = (6·x3 + 2·x2 – 6·x3 – 4·x2 + 8·x)/x^4 = (8·x – 2·x2)/x^4 = 2· (4 - x)/x3.
7
3. Solve the inequality y’ > 0 and y’ <0:
(4 - x)/x3 > 0;
(4 - x)/x3 < 0.
8
4. The left part of the inequality has one real root x = 4 and goes to infinity at x = 0. Therefore, the value x = 4 is included in a period of increasing functions in the interval descending, and point 0 is not included anywhere.
Thus, the required function is increasing on the interval x ∈ (-∞; 0) ∪ [2; +∞) and decreases with x (0; 2].