You will need
- a blank sheet of paper;
- a pen or pencil;
- the textbook on higher mathematics.
Instruction
1
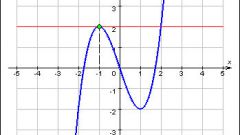
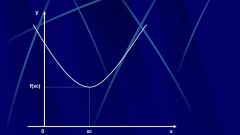
Let the function f(x) is continuous and defined on a given interval [a; b] and has on it some (finite) number of critical points. First, find the derivative function f'(x) h.
2
Equate the derivative of the function to zero to determine the critical points of the function. Do not forget to specify the point at which the derivative does not exist, they are also critical.
3
Of the many found the critical points we select those which belong to the segment [a; b]. The computed values of the function f(x) at these points and at the ends of the segment.
4
From the set of found values of the function to select the maximum and minimum values. This is the desired maximum and minimum values of the function.