Instruction
1
It is possible to consider an approximate scheme in which it is appropriate to explore the behavior of functions and to build its graph.
Find the domain of the function. Determine whether the function is even and odd. In the case of finding the right answer, continue testing, only the desired axis. Determine whether the function is periodic. In the case of a positive answer will continue to study just for one period. Find the break points of the function and determine its behavior in the vicinity of these points.
Find the domain of the function. Determine whether the function is even and odd. In the case of finding the right answer, continue testing, only the desired axis. Determine whether the function is periodic. In the case of a positive answer will continue to study just for one period. Find the break points of the function and determine its behavior in the vicinity of these points.
2
Find the point of intersection of the function with the coordinate axes. Find the asymptotes, if any. Investigate using a first derivative function for extrema and intervals of monotonicity. Also do your research by using the second derivative for convexity, concavity and points of inflection. Select points to specify the behaviour of the function and calculate the values of the function. Plot the function, considering the results obtained for all conducted researches.
3
On the axis 0X should highlight the salient point: the break point x=0 , the zeros of the function, extreme points, inflection points. In these pointx and calculate the function values (if they exist) and on the plane 0xy, select the corresponding points of the graph and the points selected for updating. A line drawn through all points is constructed, taking account of the intervals of monotony, convexity and asymptotes, and give a sketch of the graph of a function.
4
So, a specific example of the function y=((x^2)+1)/(x-1) do your research using the first derivative. Rewrite the function in the form y=x+1+2/(x-1). The first derivative is equal to y’=1-2/((x-1)^2).
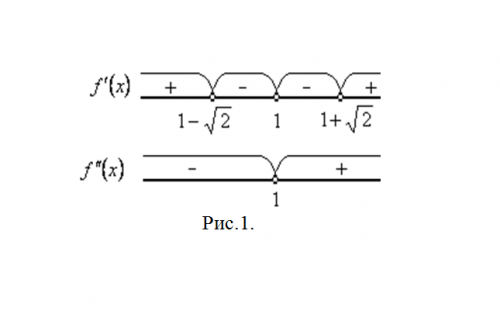
Find the critical points of the rst kind: y’=0, (x-1)^2=2, the result is two points: x1=1-sqrt2, x2=1+sqrt2. Note the measured value on the scope of the function (Fig. 1).
Determine the sign of the derivative on each of the intervals. Based on the rule of alternating signs from "+" to "-" and "-" to "+", we get that the maximum point of the function x1=1-sqrt2, and the minimum point x2=1+sqrt2. The same conclusion can be drawn and the sign of the second derivative.
Find the critical points of the rst kind: y’=0, (x-1)^2=2, the result is two points: x1=1-sqrt2, x2=1+sqrt2. Note the measured value on the scope of the function (Fig. 1).
Determine the sign of the derivative on each of the intervals. Based on the rule of alternating signs from "+" to "-" and "-" to "+", we get that the maximum point of the function x1=1-sqrt2, and the minimum point x2=1+sqrt2. The same conclusion can be drawn and the sign of the second derivative.