Instruction
1
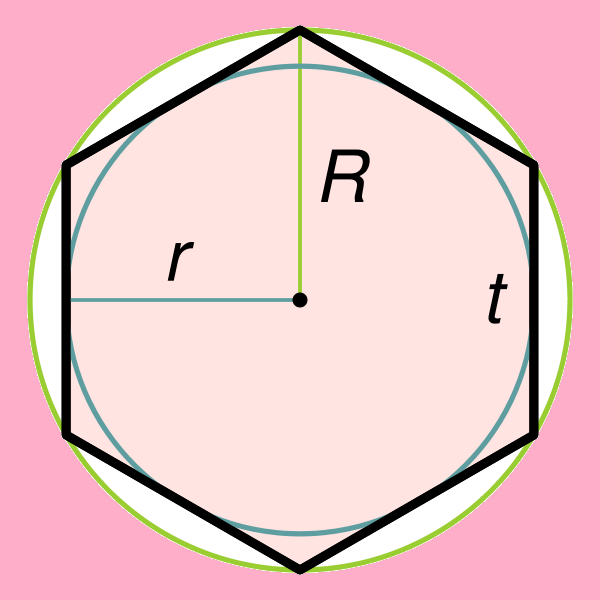
Finding the area of a regular hexagon is directly related to one of its properties, which says that around this figure can describe a circle and fit it inside this hexagon. If the inside of a regular hexagon inscribed circle, the radius can be found by the formula: r = ((√3)*t)/2, where t is the side of the hexagon. It should be noted that the radius of the circle circumscribed around the regular hexagon, is equal to its side (R = t).
2
Once is the radius of inscribed/circumscribed circle, you can begin finding the area of the desired shape. To do this, use the following formulas:
S = (3*√3*R2)/2;
S = 2*√3*r2.
S = (3*√3*R2)/2;
S = 2*√3*r2.
3
To find the area of this shape have not caused trouble, consider a few examples.
Example 1: Given a regular hexagon whose side is equal to 6 cm, it is required to find its area. For the solution you can use in several ways:
S = (3*√3*62)/2 = 93.53 cm2
The second method is more long. First, find the radius of the inscribed circle:
r = ((√3)*6)/2 = 5.19 cm
Then use the second formula to find the area of a regular hexagon:
S = 2*√3*5.192 = 93.53 cm2
As you can see, both ways are valid and do not require to check their solutions.
Example 1: Given a regular hexagon whose side is equal to 6 cm, it is required to find its area. For the solution you can use in several ways:
S = (3*√3*62)/2 = 93.53 cm2
The second method is more long. First, find the radius of the inscribed circle:
r = ((√3)*6)/2 = 5.19 cm
Then use the second formula to find the area of a regular hexagon:
S = 2*√3*5.192 = 93.53 cm2
As you can see, both ways are valid and do not require to check their solutions.
Note
It is impossible not to notice the prevalence of the form of a regular hexagon in nature. Just think of honeycomb. Almost all the complex carbon molecules have a regular hexagonal shape. Even in chemistry when portraying a molecule of benzene, used the same form.
One of the properties of a regular hexagon says: it is possible to tile any plane. This property is widely used tile pavers all countries that can pave any sidewalk tile that is hexagonal shape.
One of the properties of a regular hexagon says: it is possible to tile any plane. This property is widely used tile pavers all countries that can pave any sidewalk tile that is hexagonal shape.