You will need
- - the minimum data required to solve the problem, namely the length of each sides and diagonals of a Pentagon;
- calculator;
- - handle;
- - a sheet of paper.
Instruction
1
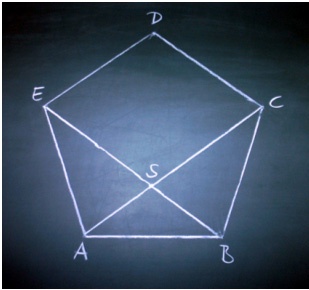
Carefully read the condition of the task. Guided by them, draw on a sheet of paper alleged the Pentagon.
2
Label the length of each of its sides.
3
Swipe in the Pentagon, two diagonals. Label the length of each diagonal.
4
Notice what happened as a result of the diagonals, and you will see that they divide the Pentagon into three distinct triangles.
5
Of the vertices of each triangle draw a height to the base.
6
Measure the length of the height lowered at the base for each triangle.
7
Determine the area of all three triangles using the formula given below:
S = ½ × H × a,
where S is the calculated area of the triangle;
H – the height of each triangle;
a – length of base of triangle.
S = ½ × H × a,
where S is the calculated area of the triangle;
H – the height of each triangle;
a – length of base of triangle.
8
Calculate the area of a Pentagonby adding together the areas of these three triangles.
Note
Remember that the right is the Pentagon, in which all sides and all angles are equal. If at least one side or angle is different from the other, the Pentagon is not considered correct, and its area cannot be calculated based on the simplified scheme.
Useful advice
The easiest way to find the area of a regular Pentagon. To do this, simply calculate the area of one of the triangles, and then multiply it by their number. Because the diagonal in the right Pentagon break it into triangles of the same area. Much easier task and in that case, if two angles of a Pentagon are straight. Enough to hold one diagonal which will divide the Pentagon into a triangle and a rectangle, the area which can be found quite simply. The sum of the calculated squares will equal the area of the Pentagon.