How to find the perimeter of the hexagon

To find the perimeter of the hexagon, measure and add the lengths of all six sides. P = A1+A2+A3+A4+A5+A6,where P is the perimeter of the hexagon, and A1, A2 ... A6 – the length of its sides.The units of each of the parties reduced to a single species, in this case, it is sufficient to store only the numerical values of the lengths of the sides. The unit of measure of the perimeter of the hexagon will coincide with the unit of measure of the parties.

Example.A hexagon with side lengths 1 cm, 2 mm, 3 mm, 4 mm, 5 mm, 6 mm. is Required to find its perimeter.Solution.1. The unit of measurement of the first side (cm) differs from the units of measurement of the lengths of the other sides (mm). Therefore, move: 1 cm = 10 mm. 2. 10+2+3+4+5+6=30 (mm).

If the hexagon is correct, then to find its perimeter, multiply the length of its side six:R = a * 6,where a is the length of sides of a regular hexagon.Example.To find the perimeter of a correct hexagon with side length equal to 10 cm Solution: 10 * 6 = 60 (cm).

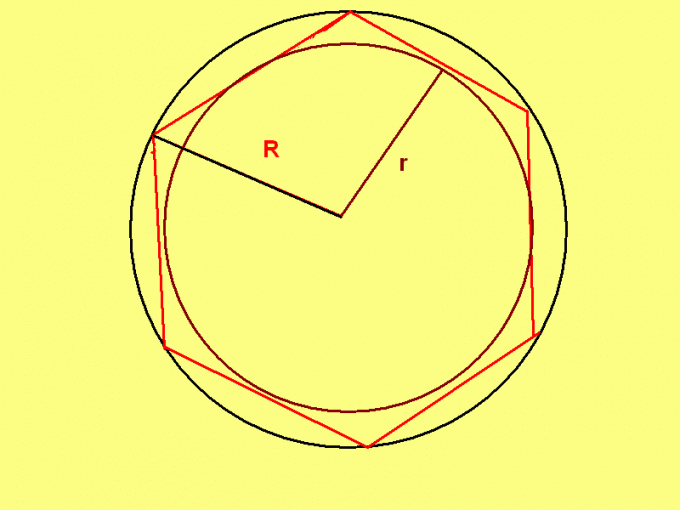
A regular hexagon has a unique feature: the radius of the circumscribed around this hexagon of a circle is equal to the length of its side. So, if you know the radius of the circumscribed circle, to use the formula:P = R * 6,where R is the radius of the circumscribed circle.

Example.To calculate the perimeter of a right hexagon, wrote in a circle of diameter 20 cm Solution. The radius of the circumscribed circle will be equal to: 20/2=10 (cm).Therefore, the perimeter of the hexagon: 10 * 6 = 60 (cm).

If a task is set to the radius of the inscribed circle, apply the formula:P = 4 * √3 * r,where r is the radius inscribed in a regular hexagon circle.

If you know the area of the right hexagon, then to calculate the perimeter use the following ratio:S = 3/2 * √3 * A2,where S – area of a regular hexagon. Here you can find a = √(2/3 * S / √3), hence:P = 6 * a = 6 * √(2/3 * S / √3) = √(24 * S / √3) = √(8 * √3 * S) = 2√(2√3).