You will need
  • - twine;
  • roulette;
  • a pair of compasses;
  • - the range;
  • calculator.
Instruction
1
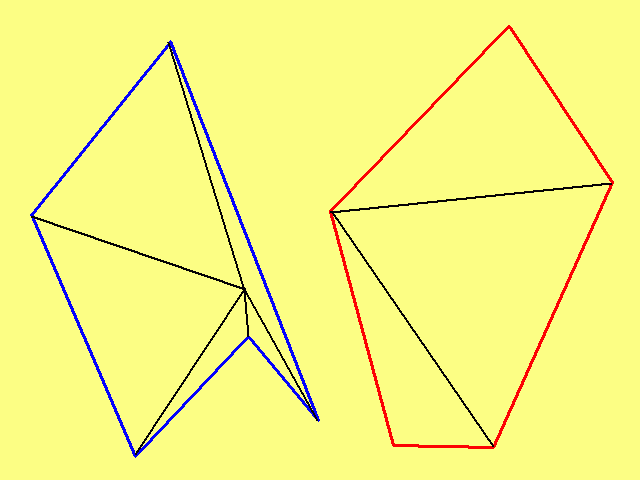
In order to calculate the area of an arbitrary polygon, mark the inside arbitrary point, and then connect it with each vertex. If the polygon is non-convex, select a point so that held the segments did not cross the figure. For example, if the polygon is the outer boundary of the "stars" that point need not be noted in the "ray" star in its center.
2
Now measure the lengths of the sides in each of the resulting triangles. Then use the Heron formula and calculate the area of each of them. The sum of the areas of all the triangles is the required area of the polygon.
3
If the shape of a polygon is a figure very large area, for example, land, to hold segments of desired length will be rather problematic. Therefore, in this case, proceed as follows: beat in the center of the polygon and drag a peg from it to every vertex cut of twine. Then measure and record in sequence the lengths of all the segments. Similarly, measure and sides of the polygon, pulling the string between adjacent nodes.
4
To use the Heron formula, first calculate properiter each triangle by the formula:

p = ½ * (a + b + C),

where:
a, b and c are the lengths of the sides of the triangle
R – properiter (standard notation).

Defining properiter triangle, substitute the number into the following formula:

S∆ = √(p*(p-a)*(p-b)*(p-c)),

where:
S∆ is the area of a triangle.
5
If the polygon is convex, i.e. has interior angles exceeding 180º, then choose an internal point of any vertex of the polygon. In this case, triangles will two less, which sometimes can significantly simplify the task of finding the area of a polygon. The calculation of the areas of the resulting triangles does not differ from that described above.
6
When solving school tasks and "tasks of thinking" look at the shape of a polygon. Perhaps it can be broken into several parts which can be folded "right" shape, e.g., square.
7
Sometimes a polygon can be "complement" to the right of the figure. In this case, simply subtract the area of the enlarged shape square add-ons. By the way, this method is relevant not only to solve abstract problems. For example, if the corners and along the walls of the room you have placed furniture for calculating free area, simply subtract from the total area of the room, the area occupied by furniture.