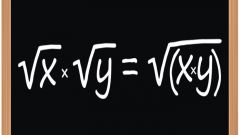You will need
- the roots of a given degree;
- - handle;
- - a sheet of paper;
- calculator.
Instruction
1
Carefully read the conditions of the job and analyze data. Pay attention to exponents. From different or the same, depends on the mode of action. If you want to multiply roots of the same degree, just multiply between a radical expression. It doesn't matter how many roots you have. The exponent remains the same. For example, you need to multiply the square roots of the numbers a, b and c. The expression will look like: √a*√b*√c = √abc.
2
Division of roots with equal exponents are the same. Put the root with the same index. One radical expression divide to another. √a : √b=√a/b. Instead of a and b can be any number or letter designations. Above the sign of the root private place that same exponent that the dividend and divisor.
3
If the exponents are different, the calculations necessary to carry out a little differently. The exponents in this case are also involved in the process. They must lead to total about the same as is done when converting fractions. If you need to perennite the roots with the indices m and n, the total rate is mn. Accordingly, the first factor you need to build in a degree n both numbers. Multiply the exponents of the radical of this additional factor. In the second case, multiply both figures by m. Place the radical sign with the index mn, and multiply radical expressions as in the first method. The division is similar.
4
If the roots are the ratios, they must multiply or divide separately. Write the result before the root sign, which is the result of the multiplication or division of radical expressions.
5
Very often it is necessary to withdraw one of the factors under the root or Vice versa. For this, the number before the radical, it is necessary to erect to the same degree, which is indicated by the indicator and remove the roots. For example, 3√2=√9*2=√18. You can do the opposite, expanding radical expression for cofactors. Extract the square root of that factor, from which it can be done, and remove it from under the radical sign.
Note
Such actions have meaning only if the radical expression is presented a non-negative number.