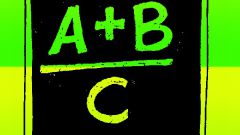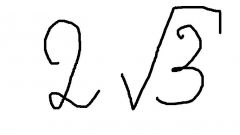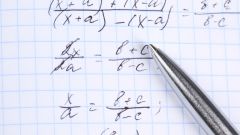Instruction
1
Before you get rid of irrational fractions in the denominator, determine its type, and depending on that to continue the solution. And though any irrationality follows from the mere presence of the roots, their various combinations and degrees imply different algorithms.
2
The square root in the denominator, the expression a/√bВведите additional factor of √b. That fraction has not changed, and you need to multiply the numerator and the denominator:a/√b → (a•√b)/b.Example 1: 10/√3 → (10•√3)/3.
3
Availability under the line of a fraction root of a fractional exponent of the form m/n, where n>meto expression as follows:a/√(b^m/n).
4
Get rid of such irrationality also by entering a multiplier, this time more complex: b^(n-m)/n, i.e. the exponent of the root and subtract the degree of the expression under its sign. Then the denominator will be only the first degree:a/(b^m/n) → a•√(b^(n-m)/n)/b.Example 2: 5/(4^3/5) → 5•√(4^2/5)/4 = 5•√(16^1/5)/4.
5
The sum of the square karaulnoye components of both fractions on the same difference. Then the irrational roots of the denominator summation is converted into a difference expression/numbers under the root sign:a/(√b + √c) → a•(√b - √c)/(b - c).Example 3: 9/(√13 + √23) → 9•(√13 - √23)/(13 - 23) = 9•(√23 - √13)/10.
6
The sum/difference of cubic carnavalera as an additional multiplier partial squared difference, if the denominator is the amount, and accordingly an incomplete square of the sum of the difference of the roots is:a/(∛b ± ∛c) → a•(∛b2 ∓ ∛(b•c) + ∛c2)/ ((∛b ± ∛c)• ∛b2 ∓ ∛(b•c) + ∛c2) →a•(∛b2 ∓ ∛(b•c) + ∛c2)/(b ± c).Example 4: 7/(∛5 + ∛4) → 7•(∛25- ∛20 + ∛16)/9.
7
If the task is present and the square and cube root, then divide the solution into two steps: sequentially output from the denominator of the square root and then cube. This is done in the already known methods: in the first step is to choose the multiplier of the difference/sum of the roots, the second is an incomplete square of the sum/difference.