How to find coordinates of the vertex of the parabola

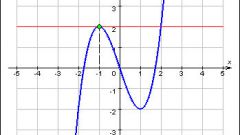
A quadratic function in General form is written by the equation: y = ax2 + bx + c. The graph of this equation is a parabola whose branches are directed upwards (if a > 0) or down (when a < 0). Students are invited to learn the formula calculate the coordinates of the vertex of the parabola. Vertex of a parabola lies at the point x0 = -b/2a. Substituting this value in the quadratic equation, get y0: y0 = a(-b/2a)2 - b2/2a + c = - b2/4a + c.

To people familiar with the concept of the derivative, it is easy to find the vertex of a parabola. Regardless of the position of the branches of the parabola, its vertex is an extremum point (a minimum, if the branches are directed upwards, or high, when the branches are directed down). To find the point of the intended extremum of any function, it is necessary to calculate its first derivative and equate it to zero. In General, the derivative of a quadratic function equal to f'(x) = (ax2 + bx + c)' = 2ax + b. Equating to zero, you get 0 = 2ax0 + b => x0 = -b/2a.

Parabola - a symmetrical line. The axis of symmetry passes through the vertex of the parabola. Knowing the point of intersection of the parabola with the axis of X, you can easily find the abscissa of the vertex x0. Let x1 and x2 - the roots of the parabola (so-called point of intersection of the parabola with the abscissa axis, since these values to draw quadratic equation ax2 + bx + c to zero). Let |x2| > |x1|, then the vertex of a parabola lies halfway between them and can be found from the following expressions: x0 = ½(|x2| - |x1|).