Instruction
1
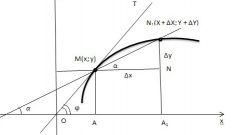
To find the coordinates of a point belonging to a straight line, click the line and drop a perpendicular line on a coordinate axis. Determine which number corresponds to the intersection point, the intersection with the axis ox is the value of the abscissa, that is x1, the intersection with the axis OU is the ordinate Y1.
2
Try to choose a point whose coordinates can be determined without fractional values for convenience and accuracy of calculations. To build the equation you need at least two points. Find the coordinates of another point belonging to a given line (x2, Y2).
3
Substitute the coordinate values in the equation of the line having the General form y=kx+b. You'll have a system of two equations Y1=kx1+b and y2=kx2+b. Solve this system, for example, the following method.
4
Express b from the first equation and substitute into the second, find k, substitute in any equation and find b. For example, the solution of the system 1=2k+b and 3=5k+b would be: b=1-2k, 3=5k+(1-2k); 3k=2, k=1.5, b=1-2*1,5=-2. Thus, the equation of the line has the form y=1.5 x-2.
5
Knowing two points belonging to direct, try, use the canonical equation of a line, it looks like this: (x - x1)/(x2 - x1)=(u - U1)/(U2 - U1). Substitute values (x1, Y1) and (x2;Y2), simplify. For example, the point (2;3) and (-1;5) owned direct (x-2)/(-1-2)=(have-3)/(5-3); -3(x-2)=2(y-3); 3x+6=2Y-6; 2Y=12-3x or y=6-1,5 H.
6
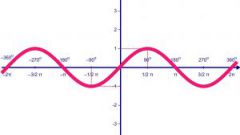
To find the equation of a function with a non-linear graph, follow these steps. See all standard graphs of y=x^2, y=x^3, y=√x, y=sinx, y=cosx, y=tgx, etc. If one of them reminds you of your schedule, take it as a basis.
7
Draw on the same axes graph the standard functions of the base and find its difference from the timetable. If chart moved a few units up or down – so features added to this number (e.g. y=sinx+4). If the graph moved right or left, so the number added to the argument (e.g., y=sin (x+P/2).
8
An elongated chart height chart says that a function argument is multiplied by some number (for example, y=2sinx). If the schedule, on the contrary, reduced in height, so the number before the function less than 1.
9
Compare the graph of the function-the basics and your options on width. If it is more narrow, then x is a number greater than 1, a wide – number less than 1 (e.g., y=sin0.5x).
10
Substituting into the function equation for different values of x, check whether there is a value of the function. If everything is correct - you podpali the function equation on the schedule.