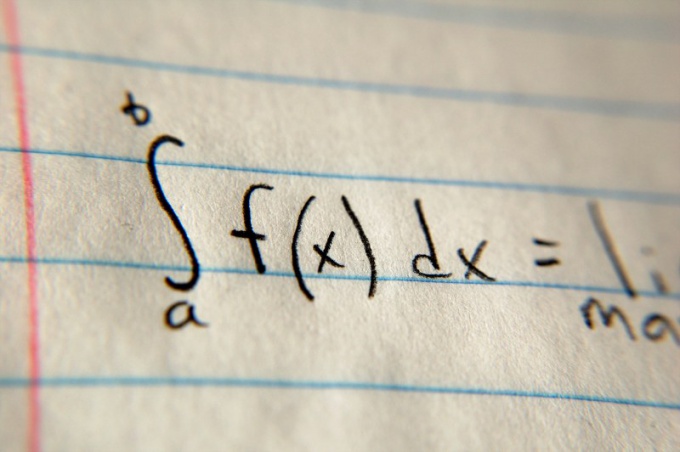How to calculate the area of the figure bounded by the parabola

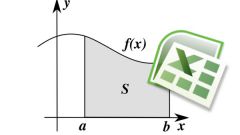
To calculate the area of the figure bounded by the parabola, draw it in the Cartesian coordinate system. For the image of the parabola should know a minimum of three points, one needs to be a top. To find the coordinate of the vertices along the X-axis, substitute the known data into the formula x=-b/2a, Y-axis, substitute the obtained value of the argument to the function. After that, analyze the graphics data included in the problem statement. If the vertex is below the x axis, the branches are directed upwards, if the above — down. The remaining 2 points are coordinates of intersection with the axis OX. Stroke resulting figure. This will greatly facilitate the solution of this problem.

Then, determine the limits of integration. They are usually specified in the problem statement using variables a and b. These values are put in the upper and lower parts of the symbol of the integral, respectively. After the integral, enter the value of the function and multiply it by dx (for example, (x2)dx in the case of the parabola). Then calculate the integral value of a function in General form using a special table at the link given in the section "Additional sources", and then substitute back the limits of integration and find the difference. The difference will be the area.

There is also the possibility of calculating the integral and using software. To do this, follow the link in the section "Additional sources", a special mathematical website. In the open text box, enter the integral of f(x), where f(x) — recording function, the schedule limits the area of the figure on the coordinate plane. After that press the button with the symbol equal to. The opening page portray the resulting figure, and show the calculations of its area.