Instruction
1
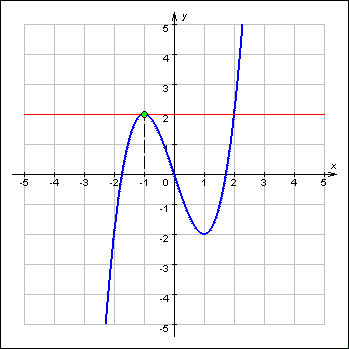
Write the given function f(x). Define its first derivative f’(x). The obtained expression of the derivative Paranaita to zero.
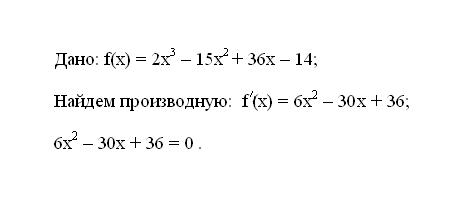
2
Solve the resulting equation. The roots of the equation will be the critical points of the function.
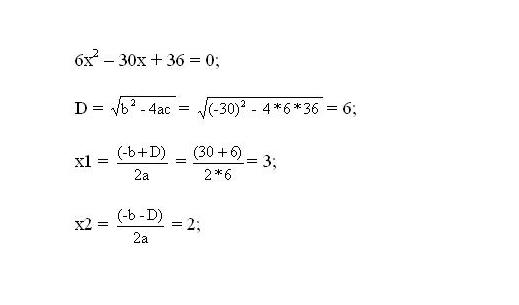
3
Determine the critical points of maximum or minimum are obtained roots. To do this, find the second derivative f’(x) from the original function. Substitute it in turns to the critical point and calculate the expression. If the second derivative of the function at the critical point is greater than zero, it will be a minimum point. Otherwise the maximum point.

4
Calculate the value of the original function to the obtained points of minimum and maximum. To do this, substitute their values in the expression for the function and calculate. The resulting number will determine the extremum of the function. Moreover, if the critical point was a maximum, the extremum of the function will also be high. Also, the minimum critical point, the function will reach its minimum extremum.