Instruction
1
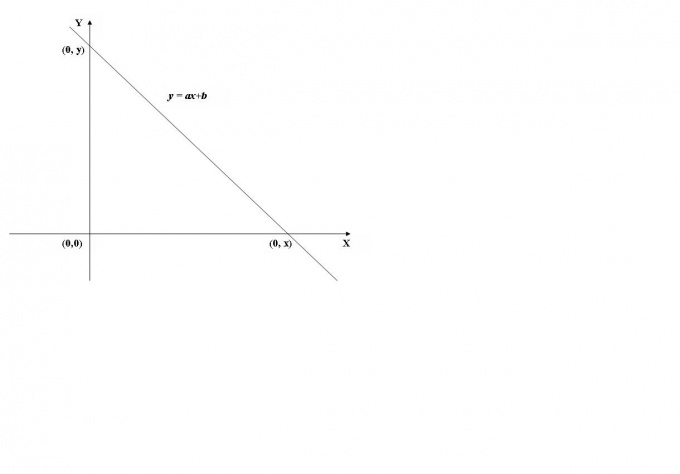
To find the point of intersection of the function with the y-axis, you must calculate the value of the function at x=0, i.e. find f(0). For example, you will use the graph of the linear function depicted in Fig.1. Its value at x=0 (y=a*0+b) is equal to b therefore, the graph crosses the y-axis (Y-axis) at the point (0,b).
2
At the intersection of the abscissa (X-axis) the value of the function is 0, i.e., y=f(x)=0. To calculate x you need to solve the equation f(x)=0. In the case of linear functions we obtain the equation ax+b=0, whence we find x=-b/a.
Thus, the X-axis intersects at the point (-b/a,0).
Thus, the X-axis intersects at the point (-b/a,0).
3
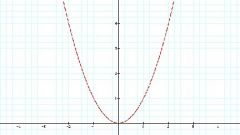
In more complex cases, for example, in the case of quadratic dependence of y from x, the equation f(x)=0 has two roots, therefore, the x-axis is crossed twice. In the case of a periodic dependence y from x, for example y=sin(x), its graph has an infinite number of points of intersection with the axis X.
To check the correctness of the finding of the coordinates of the points of intersection of the function with the X-axis you need to substitute the values of x in the expression f(x). The value of the expression when any of the computed x should be 0.
To check the correctness of the finding of the coordinates of the points of intersection of the function with the X-axis you need to substitute the values of x in the expression f(x). The value of the expression when any of the computed x should be 0.