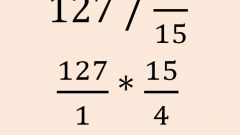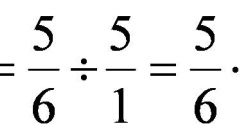You will need
- calculator
Instruction
1
Look closely at these numbers. If some fractions have decimal and narvilene, it is sometimes easier to first perform operations on decimal, and then convert them into the wrong kind. Translate fraction in the species initially recorded value after the decimal point in the numerator and putting a 10 in the denominator. If necessary, simplify the fraction by dividing the number above and below the line on one divider. Fraction, which is a part, lead to the wrong kind, multiplying it by the denominator and adding the result to the numerator. This value will become the new numerator of the fraction. To highlight a part of the original improper fraction, we must divide the numerator by the denominator. A result record to the left of the fractions. And the remainder becomes the new numerator, the denominator of the fraction is not changed. For fractions with integer part may perform actions separately, first for a and then for the decimal parts. For example, the sum of 1 2/3 and 2 ¾ can be calculated in two ways:
- The transfer of the fractions in improper form:
- 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
Summation of separate integral and fractional parts of terms:
- 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾ ) = 3 +(8/12 + 9/12) = 3 + 17/12 = 3 + 1 5/12 = 4 5/12.
- The transfer of the fractions in improper form:
- 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
Summation of separate integral and fractional parts of terms:
- 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾ ) = 3 +(8/12 + 9/12) = 3 + 17/12 = 3 + 1 5/12 = 4 5/12.
2
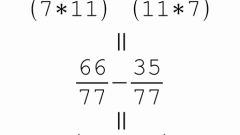
For improper fractions with different values under the dash, find the common denominator. For example, 5/9 and 7/12 common denominator will be 36. To do this, the numerator and denominator of the first fraction should be multiplied by 4 (it will 28/36) and second on 3 (get 15/36). Can now perform the necessary calculations.
3
If you are going to calculate the sum or difference of fractions, first record found the common denominator under the line. Perform the required actions in between the numerators and write the result above the line of the new fraction. Thus, the new numerator will be the difference or the sum of the numerators of the original fractions.
4
To calculate the product of the fractions multiply the numerators of the fractions and write the result in place of the numerator of the final fraction. Do the same for the denominators. When dividing one fraction to another write down one fraction, and then multiply the numerator by the denominator of the second. The denominator of the first fraction is multiplied respectively to the numerator of the second. Thus there is a kind of revolution of the second fraction (divisor). The resulting fraction will consist of the results of multiplying the numerators and denominators of both fractions. It is easy to learn how to solve fractionsrecorded in the condition in the form of "four-storied" fraction. If a trait is shared by the two fractions, rewrite them using the delimiter ":" and continue with the usual division.
5
To obtain the final result, reduce the fraction, divide the numerator and the denominator by a single integer, the largest possible in this case. While above and below this line must be integers.
Note
Do not perform arithmetic operations with fractions, the denominators are different. Choose a number that when multiplied by it, the numerator and denominator of each fraction in the result, the denominators of both fractions were equal.
Useful advice
When writing fractional numbers the numerator is written above the line. This value is referred to as the numerator of the fraction. Below the line is written to the divisor, or denominator, of the fraction. For example, half a kilogram of rice as a fraction written in the following way: 1 ½ kg of rice. If the denominator is equal to 10, such a fraction is called a decimal. The numerator (dividend) is written to the right of the integer part using a comma: 1.5 kg of rice. For computational convenience, such a fraction can always be written in an incorrect form: 1 2/10 kg of potatoes. To simplify, you can reduce the values of the numerator and denominator by dividing them into a single integer. In this example, perhaps dividing by 2. The result is a 1 1/5 kg of potatoes. Make sure that the numbers that you are going to perform arithmetic operations, presented in the same form.