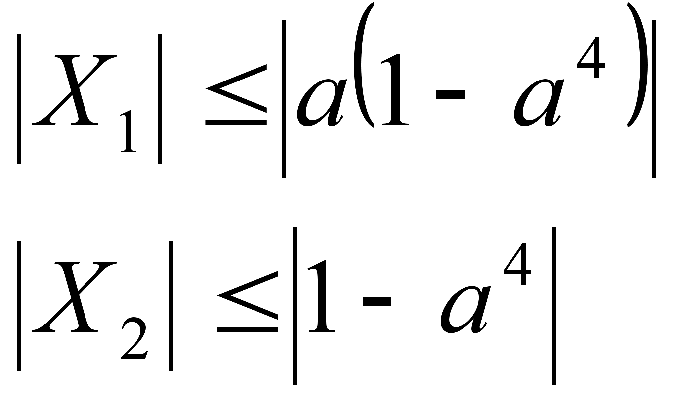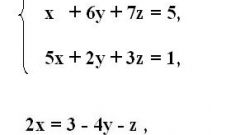Instruction
1
With the options can be equations and inequalities. In either case, we need to Express x.
Simply in such type of examples, this is not done explicitly, but using this parameter.
By itself, a parameter, more precisely, its value is a number. Settings are usually designated by the letter a. But the problem is that we don't know his module, no mark. Hence difficulties arise when working with inequalities or solving modules.
Simply in such type of examples, this is not done explicitly, but using this parameter.
By itself, a parameter, more precisely, its value is a number. Settings are usually designated by the letter a. But the problem is that we don't know his module, no mark. Hence difficulties arise when working with inequalities or solving modules.
2
However, it is possible (but beware, pre-noting all possible restrictions) apply all the usual methods of working with equations and inequalities.
And, in principle, the expression x through and usually takes a lot of time and effort.
But writing the full answer is much more laborious and time-consuming process.
And, in principle, the expression x through and usually takes a lot of time and effort.
But writing the full answer is much more laborious and time-consuming process.
3
The fact that, in connection with ignorance of the value of the parameter, we must consider all possible cases for all values of a from minus to plus infinity.
Here we can use graphical method. Sometimes called "coloring". It lies in the fact that we are in x(a) (or a(x) as the image represented by lines, the resulting transformation of our original example. And then we begin to work with these lines: since the a value is not fixed, we need the line containing in its equation a parameter shift on schedule, in parallel to tracking and calculating points of intersection with other lines, as well as analyzing the signs of the areas they are suitable for us or not. Suitable for convenience and clarity, let's shade.
Thus, we pass the entire number line from minus to plus infinity, checking the answer for all.
Here we can use graphical method. Sometimes called "coloring". It lies in the fact that we are in x(a) (or a(x) as the image represented by lines, the resulting transformation of our original example. And then we begin to work with these lines: since the a value is not fixed, we need the line containing in its equation a parameter shift on schedule, in parallel to tracking and calculating points of intersection with other lines, as well as analyzing the signs of the areas they are suitable for us or not. Suitable for convenience and clarity, let's shade.
Thus, we pass the entire number line from minus to plus infinity, checking the answer for all.
4
The written response similar to the response for the method of intervals with a certain caveat: we don't just define a set of solutions for x, and write some set of values and corresponds to how many values of X.