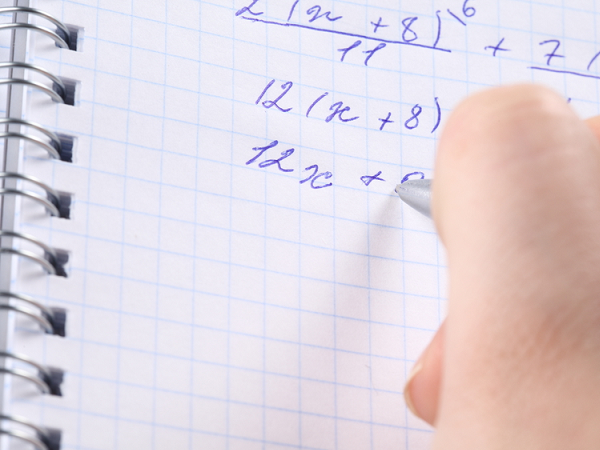Instruction
1
The concept of universal norms for any matrix, square or non-square, matrix-row-or column, the dimension also can be any. This characteristic is used as estimate for variability analysis of the matrix in any design process or a combination of several matrices.
2
We can say that the norm is indicative of the "power" of the matrix. It is denoted by ‖A‖ and the actual number that should match a specific set of conditions:‖A‖ ≥ 0, with equality to zero occurs only for the zero matrix;‖a•a‖ = ‖a‖•‖A‖, where a belongs to the set of rational numbers;‖A+b‖ ≤ ‖A‖ + ‖In‖ - commutativity.
3
The norm being also the property ‖A•‖ ≤ ‖A‖ • ‖In‖, is called multiplicative. There are three types of rules: infinite, the first and Euclidean. All of them are canonical, i.e., their values are not less in any module of the matrix element. In practice we usually compute only one of the types, this is sufficient for an objective assessment.
4
To find the norm of the matrix, you have to use one of the following methods for each species. They are all based on calculating the sum of the elements of the matrix, but each involves a custom algorithm.
5
To calculate the infinite norm sum modulo the values of the elements separately for each row and choose the maximum of them:‖A‖_1 = mAh Σ_j |a|.
6
Locate the first rulein doing similarly with the elements in each column:‖A‖_2 = mAh Σ_i |a|.
7
The calculation of the Euclidean norm implies three steps: the construction of each element to the square, summing and square root of the total result is:‖A‖_3 = √Σа2_ij.
8
Example: calculate all kinds of rules for a given matrix.
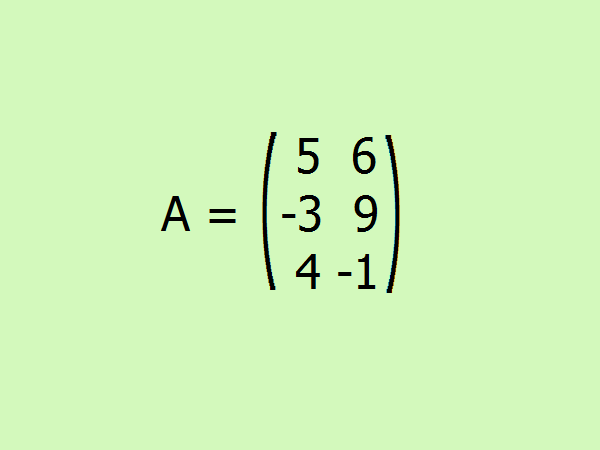
9
Решениеа11+a12=11; a21+a22=12; a31+a32=5 → ‖And‖_1 = 12;a11+a21+a31=12; a12+a22+32=16 → ‖And‖_2 = 16;‖And‖_3 = √(25+36+9+81+16+1) = √168 ≈ 13.