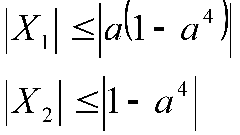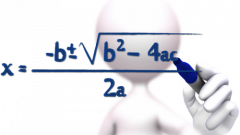Instruction
1
The expression value of the formula is performed using mathematical operations – transfer members, dividing one number by both parts of records etc. that is, should be simplified and work with the formula as an algebraic equation. Performing these actions, you must also take into account the change of sign, the rules of inference of the value of under root, exponentiation.
2
In the most simple case expressions of the form v = 2*g + 11 for finding the magnitude of g, perform the following steps. Move all members that do not contain the variable g in one (preferably left) part of this equation, not forgetting to change the sign when transferring to the opposite: -2*g = 11 - v. Other quantities and constants move over the equal sign. If desired quantity is the coefficient in this case (-2), divide by this constant to both sides of the equation: g = -(11 – v)/2.
3
In terms of formula size, raised to a power, as, for example, in the following form: S = a*t2/4, do the first of the above described actions. Put a variable in the degree on the left side of the equation, and to output the constants from the denominator of the fraction multiply by this number, both parts of the formula: a*t2 = 4*s. Divide equation into the variable a and get: t2 = 4*S/a. To remove a degree of the desired variable, take the root of the same degree (here square) on the left and right subexpressions: t = √4*S/a. Also found the reverse situation, when the desired value is under the sign of the root, in this case you need to carry out the construction of the whole equation to the power specified the root. So, the expression 3√S = v + g is converted into the form S = (v + g)3.
4
If you have a complex expression obtained as a result of multiple substitutions of different formulas, there are often difficulties in expressing the unknown variable. For example, in the design of the form S = (√t2*k/(1+g))*f – 15 when searching for a value k, it is desirable to carry out a preliminary simplification of the equations by introducing a wildcard variable. Take for x the expression in large parentheses: x = (√t2*k/(1+g)), then the original equation would look like this: S = x*f – 15. Easy is x = (S + 15)/f. Next return is x bracket expression (√t2*k/(1+g)) = (S + 15)/f . You can then continue to simplify by using a similar lookup or just to Express the desired value: k = ((1+g)*(S + 15)/f )2/t2.