You will need
  • Drawing cone with the specified parameters
  • Line
  • Pencil
  • Math formulas and definitions
  • The height of the cone
  • The radius of the circular base of the cone
  • Formula of area of triangle
Instruction
1
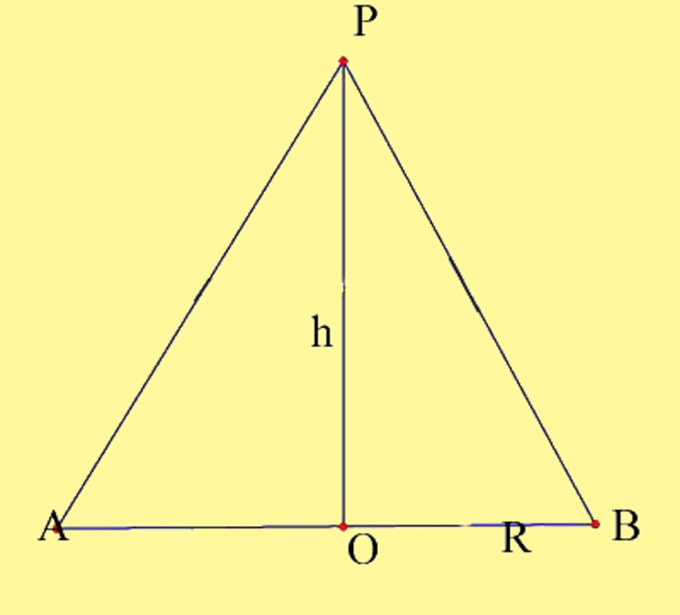
Draw a cone with the specified parameters. Mark the center of the circle as O and the top of the cone — like P. You need to know the base radius and height of the cone. Summarize the properties of the height of the cone. It is a perpendicular drawn from the vertex of the cone to its base. The point of intersection of the height of the cone with the plane of the base in a direct cone coincides with the center of circular base. Build an axial section of the cone. It is formed of the base diameter and forming a cone that pass through the point of intersection of the diameter with the circumference. Denote the resulting points as A and B.
Build an axial section of the cone
2
Axial section is formed by two rectangular triangles lying in one plane and having one common side. Calculate the area of the axial section in two ways. The first method is to find the areas of the resulting triangles and put them together. This is the most obvious way, but in fact it does not differ from the classical calculation of the area of an isosceles triangle. So you have 2 right triangles, a common side which is the height of the cone h, the second the legs are the radii of the circular base R and hypotenuse — forming cone. Since all three sides of these triangles are equal, then the triangles also turned out to be equal, according to the third property of equality triangles. The area of a right triangle is equal to half the works of the other two sides, that is, S=1/2Rh. The area of the two triangles, respectively, will be equal to the product of the radius of the circular base to a height, S=Rh.
3
Axial section are often regarded as an isosceles triangle, a height which is the height of the cone. In this case, the triangle of art, whose base is equal to the diameter of a circle base of the cone D, and the height equal to the height of the cone h. Its area is calculated by the classic formula of area of triangle, that is, in the end we get the same formula S = 1/2Dh = Rh, where S is the area of an isosceles triangle, R is the radius of the circular base and h is the height of the triangle and is the height of the cone.