How to calculate the volume of a cone

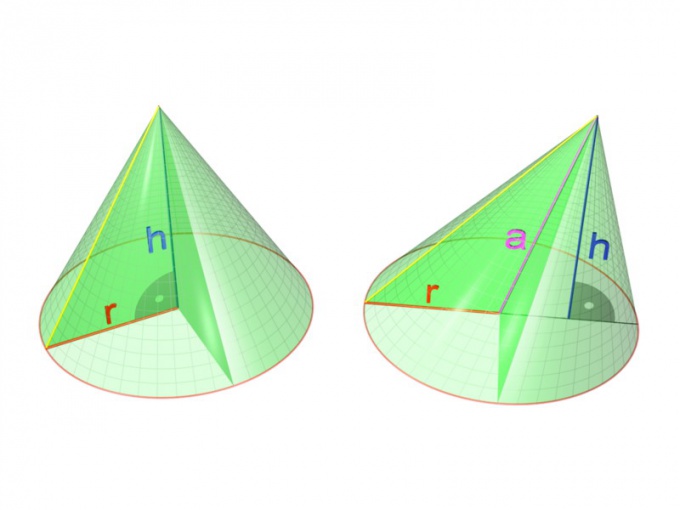
The cone can be set in different ways. For example, it may be known to the radius of its base and the length of the side. Another option is the base radius and height. Finally, another way of setting a circular cone is to specify the vertex angle and height. As is easily seen, all these methods define a circular cone by far.

Most often known for the base radius and the height of the cone. In this case, you must first calculate the area of the base. According to the formula of the circle it will be equal to NR^2, where R is the base radius of the cone. Then the volume of the body is equal to NR^2*h/3 where h is the height of the cone. This formula is easily checked using the integral calculus. Thus, the volume of a circular cone is exactly three times less than the volume of cylinder with same base and height.

If the height is not specified, and instead the known base radius and the length of the sides, to determine the amount you initially have to find the height. Since the lateral side is a hypotenuse of a right triangle, and the radius of the base serves as one of the other two sides, then the height will be the second leg of the same triangle. By the Pythagorean theorem h = √(l^2 - R^2), where l is the length of the sides of the cone. It is obvious that this formula will make sense only when l ≥ R. if l = R, then the height becomes zero, since the cone in this case turns in a circle. If l < R, the existence of such a cone impossible.

If you know the angle at the vertex of the cone and its height, then volume will need to find the radius of the base. To do this, you will have to refer to the geometrical definition of the cone-like body formed by rotation of a right triangle. In this known angle at the vertex is twice the corresponding angle of the triangle. Therefore, the angle at the vertex it is convenient to denote 2α. Then the angle of triangle will be equal to α.

By definition of the trigonometric functions of the desired radius is equal to l*sin(α), where l is the length of the sides of the cone. At the same time, known according to the problem height of the cone equal to l*cos(α). From these equalities it is easy to derive that R = h/cos(α)*sin(α) or, equivalently, R = h*tg(α). This formula always makes sense, since the angle α being an acute angle of a right triangle will always be less than 90°.