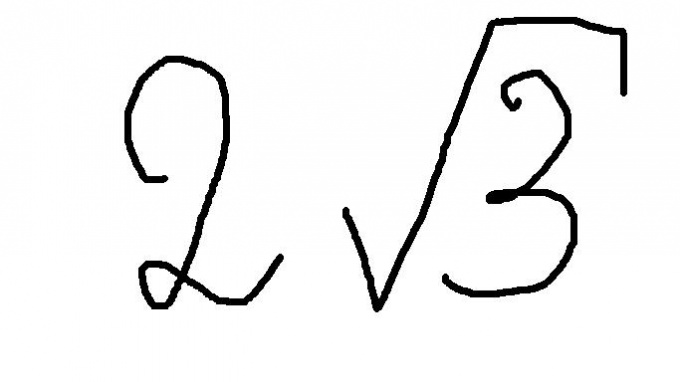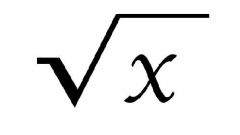Instruction
1
Look at your root. If the numberrecorded under the root is a perfect square of another number (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ... ), remove the root. That is find such a whole number, the square of which is the numberrecorded under the root. Multiply it by the second multiplier. Write down the answer.
2
If the square root is not removed, then usually the answer can be recorded by simply removing the multiplication sign. It turns out the numberconsisting of an integer and a nearby root. This will mean that this root is taken such that an integer number of times. A whole number is usually written to the left of the root.
3
If you want all the number to enter under root, do the following. Construct the whole piece into a square. Comnote on the number, standing under a root. Note the resulting number under the root. This will be your answer.
Note
Square root - a root of degree 2. If the task uses the roots as much as other degrees, change the necessary extent in the solution algorithm.
Useful advice
Recommend you often look in your math textbook. There you will find a lot of useful and valuable information that will surely help you in solving mathematical problems.