Instruction
1
About the use of the calculator will not speak, although, of course, in many cases it is simply necessary.
So, the square root of the number x is the number y, which squared gives the number x.
Definitely need to remember one very important point: the square root is computed only from positive numbers (not complex take). Why? See the definition written above. The second important point: the result of the root extraction if there are no additional conditions in the General case there are two integers: +y and -y (in the General case, the module y), as both of them squared gives the original number x, which does not contradict the definition.
The square root of zero is zero.
So, the square root of the number x is the number y, which squared gives the number x.
Definitely need to remember one very important point: the square root is computed only from positive numbers (not complex take). Why? See the definition written above. The second important point: the result of the root extraction if there are no additional conditions in the General case there are two integers: +y and -y (in the General case, the module y), as both of them squared gives the original number x, which does not contradict the definition.
The square root of zero is zero.
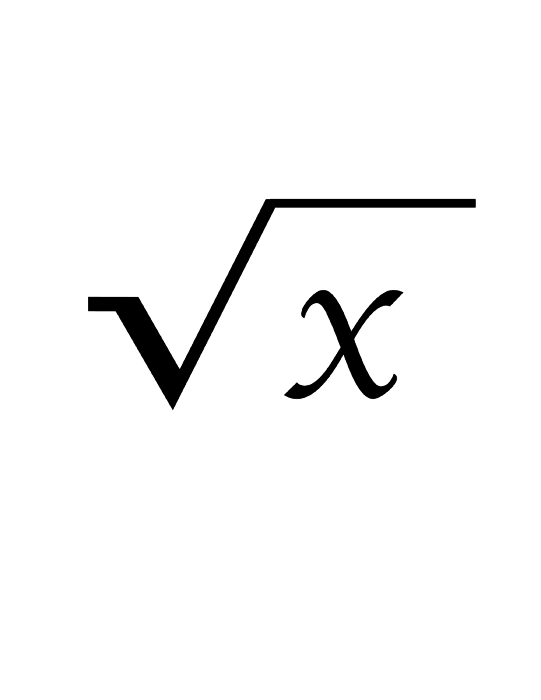
2
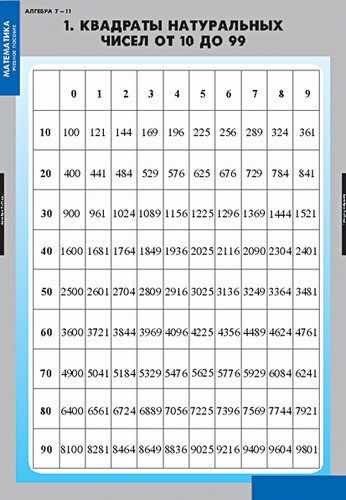
Now, with regard to specific examples. For small numbers the squares (and hence the roots as the inverse operation) it is best to remember the multiplication table. I'm talking about the numbers from 1 to 20. This will save your time and help in assessing the possible value of the desired root. For example, knowing that the root of 144 = 12, and the root of 13 = 169, we can estimate that the root of the number 155 is between 12 and 13. A similar evaluation can be applied for larger numbers, their only difference is the complexity and execution time of these operations.
Also, there is another simple fun way. Let's show it on example.
Suppose there is a number 16. Find out which number is his root. To do this, we successively subtract of the 16 primes and count the number of operations performed.
So, 16-1=15 (1), 15-3=12 (2), 12-5=7 (3), 7-7=0 (4). 4 operations – the required number 4. The essence is to carry out the subtraction as long as the difference does not become equal to 0 or will simply be deducted less than the next Prime number.
The disadvantage of this method is that thus it is possible to find only the integer part of the root, but not all of its exact meaning completely, but sometimes with a precision of estimation or errors of computation, and this is enough.
Also, there is another simple fun way. Let's show it on example.
Suppose there is a number 16. Find out which number is his root. To do this, we successively subtract of the 16 primes and count the number of operations performed.
So, 16-1=15 (1), 15-3=12 (2), 12-5=7 (3), 7-7=0 (4). 4 operations – the required number 4. The essence is to carry out the subtraction as long as the difference does not become equal to 0 or will simply be deducted less than the next Prime number.
The disadvantage of this method is that thus it is possible to find only the integer part of the root, but not all of its exact meaning completely, but sometimes with a precision of estimation or errors of computation, and this is enough.
3
Some basic properties: the root of the sum (difference) is not equal to the sum (difference) of the roots, but the root of the product of (private) equal to the product of (private) roots.
The root of the square of the number x is the number x.
The root of the square of the number x is the number x.


