You will need
- Calculator
Instruction
1
First we need to determine what species the existing power equation. It can be square, or biquadratic equation with odd degrees. It is important to look at the highest degree. If it is the second - the equation of a square if the first - line. If the highest degree of the equation is the fourth, and then there is a variable in the second degree and the coefficient, the equation is biquadratic.
2
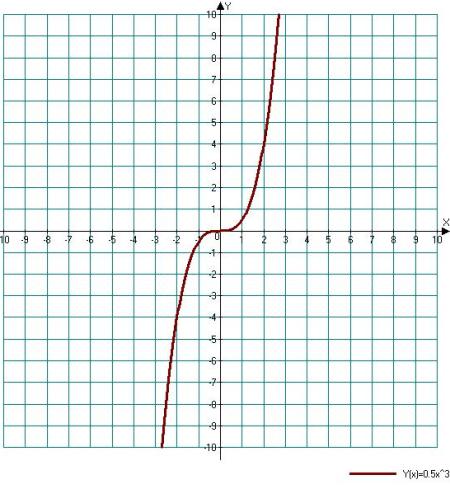
If the equation has two terms: a variable in any degree and the coefficient, the equation is solved very simple: move the variable in one part of the equation, and the number in another. Next, extract root the extent of the number which is variable. If the degree is odd, then you can record the answer, if is even, is counted and the counted number with the opposite sign.
3
To solve a quadratic equation is also quite simple. A quadratic equation is an equation of the form: a*x^2+b*x+c=0. First, consider the discriminant equation according to the formula: D=b*b-4*a*c. Everything depends on the sign of the discriminant. If the discriminant is less than zero, then we have no solutions. If the discriminant is greater than or equal to zero, we consider the roots of the equation by the formula x=(-b-sqrt(D))/(2*a).
4
Biquadratic equation like: a*x^4+b*x^2+c=0 is solved as fast as the previous two exponential equations. For this we use a substitution x^2=y, and solve the biquadratic equation as a square. We will get two y and go back to x^2. That is, we get two equations of the form x^2=a. How to solve this equation mentioned above.
Useful advice
If the equations have an odd degree, try to lead them to equations with even. To do this, divide the equation on variable one or more times. If there are no coefficients,don't forget to include the number of roots in 0.