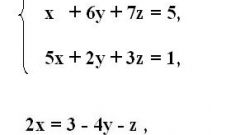Instruction
1
Cubic equation in General form looks like: ax3 + bx2 + cx + d = 0, a does not equal 0; a, b, c, d are real numbers. A universal method of solving equations of the third degree method is Cardano.
2
For starters, here is the equation to the form y3 + py + q = 0. To do this, replace the variable x by y - b/3a. Substitution replacement, see in the picture. To disclose the brackets used two formulas of reduced multiplication: (a-b)3 = a3 - 3a2b + 3ab2 - b3 and (a-b)2 = a2 - 2ab + b2. Then, given similar terms and grouped by powers of the variable y.
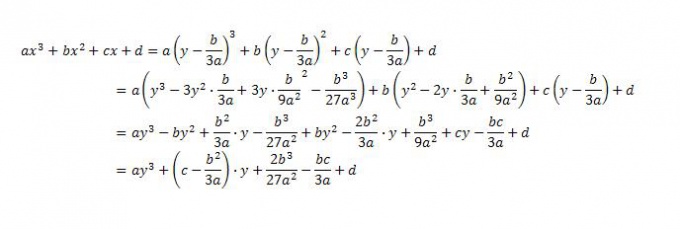
3
Now, to get under y3 unit ratio, divide all equation on a. We obtain the following formulas for the coefficients p and q in the equation y3 + py + q = 0.
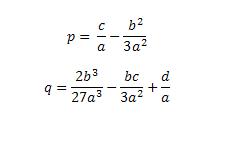
4
Then computed the special values: Q, α, β, which will allow to calculate the roots of the equation with y.
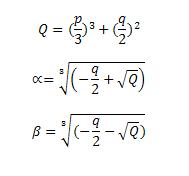
5
Then the three roots of the equation y3 + py + q = 0 are calculated by the formulas in the figure.
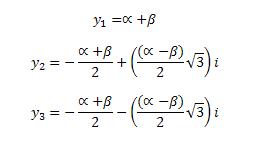
6
If Q > 0, the equation y3 + py + q = 0 has only one real root y1 = α + β (and two complex, evaluate them according to prescribed formulas, if necessary).
If Q = 0, all roots real and at least two of them coincide, with α = β and equal roots: y1 = 2α, y2 = y3 = -α.
If Q < 0 then the roots are real, but you need the ability to extract the root of a negative number.
After finding y1, y2 and y3, substitute them into the substitution x = y - b/3a and find the roots of the original equation.
If Q = 0, all roots real and at least two of them coincide, with α = β and equal roots: y1 = 2α, y2 = y3 = -α.
If Q < 0 then the roots are real, but you need the ability to extract the root of a negative number.
After finding y1, y2 and y3, substitute them into the substitution x = y - b/3a and find the roots of the original equation.
Useful advice
If you can find one of the roots of the cubic equation x1, it can be a cubic polynomial divided by (x - x1) and solve the resulting quadratic equation.