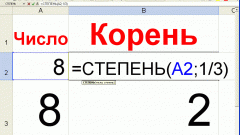
Instruction
1
So, in order to solve the cubic equation of the form Ах3+Вх2+CX+D=0, you need brute force to find one of the roots of the equation. The root of the cubic equation is always one of the divisors of the free term of the equation. Thus, in the first stage the solution of the equation, you need to find all integers a for which the constant D is divisible.
2
Received integers are alternately substituted into the cubic equation instead of the unknown variable x. The number that draws the equality of the faithful, is the root of the equation.
3
One of the roots of the equation found. For further solutions to apply the method of dividing a polynomial of the binomials. Polynomial Ах3+Вх2+CX+D is divisible, and the binomials x-h where h - the first root of the equation XX). The result of the division will be a square polynomial of the form ах2+bx+C.
4
Equating the obtained polynomial to zero ах2+bx+C =0, you get a quadratic equation, the roots of which and will be the solution to the original cubic equation, i.e. x₂' ₃ ơ=(-b±√(b^2-4ac))/2a
Note
In the first stage equation, namely, finding the root of equation by the method of selection, we should not forget about the whole negative numbers, which can also be a solution of the equation.