Instruction
1
Make a note of the original cubic equation in the form: x3+a*x2+b*x+c=0. To do this, all the coefficients of the equation divide by the first coefficient with a multiplier of x3 so that it became equal to one.
2
Based on the algorithm of the method of vieta, cardan, calculate the values of R and Q according to the respective formulae: Q =(a2-3b)/9, R=(2a3-9ab+27c)/54. Moreover, the coefficients a, b and C are the coefficients of the given equation.
3
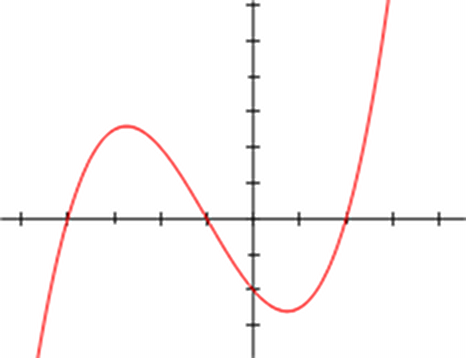
Compare the obtained values of R and Q. If it is the expression Q3 >R2 , therefore, in the initial equation there are 3 real roots. Calculate them by the formulas of vieta.
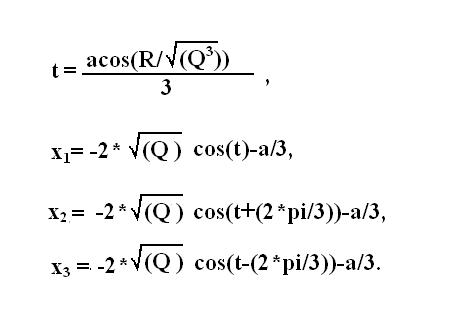
4
When Q3 values <= R2 , the solution is one real root x1 and two complex conjugate roots. To define them we need to find intermediate values A and B. Calculate their formulas Cardano.
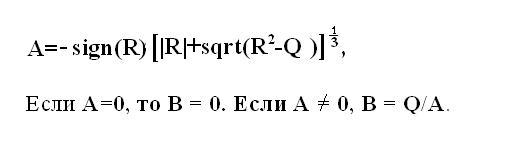
5
Find the first valid root by the formula x1=(B + A) a/3. For different values of A and b define the complex conjugate roots of the cubic equation by appropriate formulas.
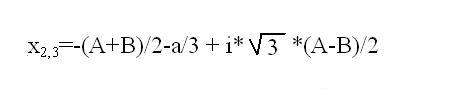
6
If the values of A and b was equal, conjugate roots, degenerate in the second real root of the original equation. This is the case when a valid root turns two. Calculate second real root by the formula x2=-A-A/3.