How to calculate the fractional degree

The calculation gives rise to fractional degrees of complexity associated with the calculations for negative numbers. In this regard, the math for dealing with fractional degree of task, you should remember a number of rules and recommendations.

$How to calculate the fractional degree$

Instruction

Make sure that the problem actually has a solution. If the basis of the degree of negative, real numbers mathematics prohibits the construction of a decimal degree. In this case, you will need to use complex calculus, which are taught at the higher technical ucebnyh institutions.

In calculating fractional exponent, there is an incident in which, on the one hand, the result of the operation -8^1/3 is not defined, but, on the other hand, we all know that the cubic root of -8 is equal to -2. However, if you try to calculate the fractional power of -8, applying the power formula A^(BC) = (A^B)^C, you can come to a contradiction: -8^1/3 = -8^2/6 = (-8^2)^1/6 = 64^1/6 = 2. Therefore, to build a negative number to a fractional exponent is forbidden, and equations should be avoided for formulas with fractional exponents, as you can lose the negative roots.

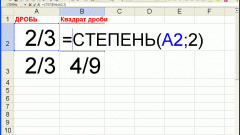
If the problem is to calculate a fractional exponent of a positive number, you can use the calculator with the function of exponentiation, for example, the standard Windows calculator. To do this, enter the base of power, then press sneak exponentiation, enter the exponent, o press the Enter key. The result will be displayed on the calculator screen.

If you want to solve an equation in which one of the arguments is present in a fractional exponent, the specific solution depends on this equation. But you need to remember a few formulas to help you calculate a fractional exponent:A^BC = (A^B)^CA^(B+C) = A^B · A^Clog(A^B) = B · log(A)

In cases when you need to find the approximate value of the fractional powers of a number, and the calculator is not at hand, use the formulas from item 4. Example: find the approximate value 100^3/5. 100^3/5 = 10^6/5 = 1000000^1/5 ≈ 1024^1/5 · 1024^1/5 = 4*4 = 16. Check on the calculator: 100^3/5 ≈ 15,85. The value obtained with good accuracy.

Is the advice useful?