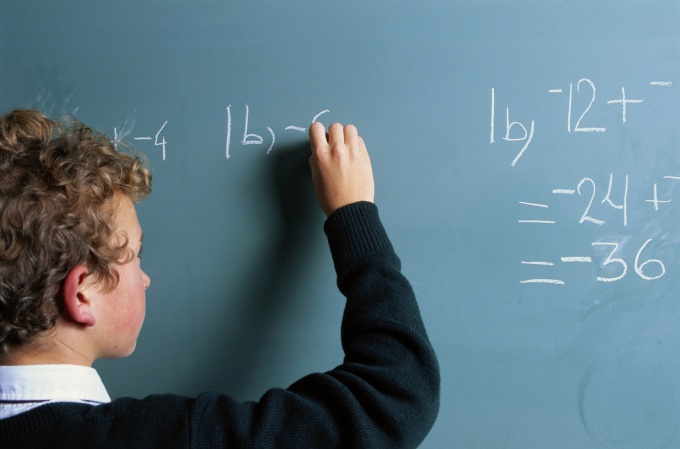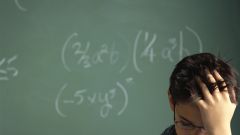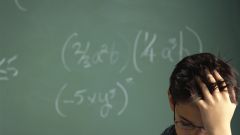Instruction
1
So you have the equation. In some part of the equation is the expression in parentheses. To expand brackets, look at the sign before the parenthesis. If the sign is plus, when the expansion of brackets in an expression record, nothing will change: just remove the brackets. If there is a minus sign, after opening the brackets you need to change all the signs in the expression, standing initially in the parentheses to the opposite. For example, -(2x-3)=-2x+3.
2
The multiplication of two brackets.
If in the equation there is the product of two brackets, opening braces occur on the standard rule. Every member of the first brackets is multiplied by every member of the second bracket. The resulting numbers are added together. The product of two "pluses" or two "cons" gives the term a plus sign, and if the multipliers have different signs, the term gets a minus sign.
Let's consider an example.
(5x+1)(3x-4)=5x*3x-5x*4+1*3 1*4=15x^2-20x+3x-4=15x^2-17x-4.
If in the equation there is the product of two brackets, opening braces occur on the standard rule. Every member of the first brackets is multiplied by every member of the second bracket. The resulting numbers are added together. The product of two "pluses" or two "cons" gives the term a plus sign, and if the multipliers have different signs, the term gets a minus sign.
Let's consider an example.
(5x+1)(3x-4)=5x*3x-5x*4+1*3 1*4=15x^2-20x+3x-4=15x^2-17x-4.
3
Opening parentheses are also sometimes called construction of expression to a degree. The formula calculates the square and the cube must know by heart and remember.
(a+b)^2=a^2+2ab+b^2
(a-b)^2=a^2-2ab+b^2
(a+b)^3=a^3+3a^2*b+3ab^2+b^3
(a-b)^3=a^3-3a^2*b+3ab^2-b^3
Formula of construction of the expression in degree more than three can be obtained with the help of Pascal's triangle.
(a+b)^2=a^2+2ab+b^2
(a-b)^2=a^2-2ab+b^2
(a+b)^3=a^3+3a^2*b+3ab^2+b^3
(a-b)^3=a^3-3a^2*b+3ab^2-b^3
Formula of construction of the expression in degree more than three can be obtained with the help of Pascal's triangle.