How to find the eccentricity

Eccentricity is called a numerical characteristic of a conic (figure obtained by the intersection of a plane and cone). The eccentricity does not change with the movement of the plane, and transformations similarity (resize when you save the form). Figuratively speaking, the eccentricity is a characteristic shape ("splashiness", in the case of an ellipse) shape, not its size.

How to find the eccentricity
How to find focus of ellipse
How to determine the type of conic curve
How to find the coordinates of intersection of altitudes in a triangle

You will need

a pair of compasses;
- the range;
calculator.

Instruction

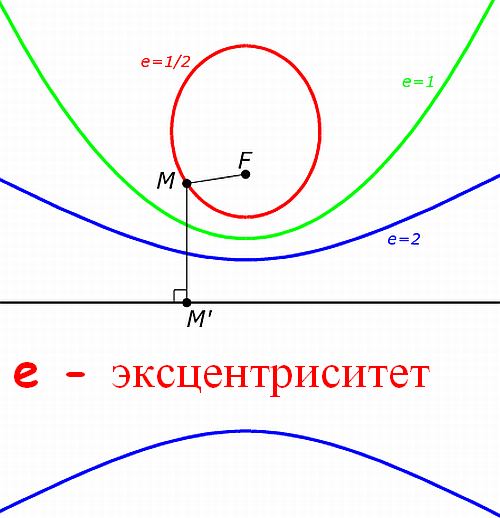
If you set the focus and directrix of a conic, to find the eccentricity, use the definition of this class of figures. All non-degenerate conic section (excluding a circle) you can build the following way:- select the plane, point and straight, set a real positive number e;- mark all points for which the distance to the selected point to straight you'll be in e times.

In this case the selected point is called a focus of a conic, straight - directrix, and the number of e - eccentricity. Depending on the value of e, obtained four types of conic sections:- if E1 – hyperbole; - if e=0 is a circle (suspended).

Based on the definition in order to find the eccentricity of the conic:- select in this figure an arbitrary point;- measure the distance between this point and the focus of the section;- measure the distance from that point to the directrix (this, lower to the directrix perpendicular, and determine the point of intersection of the directrix and the perpendicular bisector);- divide the distance from a point to focus on the distance from the point to the directrix.

If you know the length of the major and minor axes of the ellipse (its "length" and "width"), for the calculation of the eccentricity, use the following formula:e = √(1-A2/A2), where a, a – length of the minor and major axes (or axes), respectively.

If a task is set to the radii of apoapsis and periapsis of an ellipse, to find the eccentricity, use the following formula:e = (Ra-Rp)/(Ra+Rp) where Ra and Rp are the radii of apoapsis and periapsis of an ellipse, respectively (the radius of the apoapsis is the distance from the focus point of the ellipse to the most distant point; the radius of periapsis is the distance from the focus point of the ellipse to the shortest point).

If you know the distance between the foci of the ellipse and the length of its major axis, the eccentricity calculation just divide the distance between the foci to the length of the axis:e = f/A where f is the distance between the foci of the ellipse.

Is the advice useful?