Instruction
1
If F(x) is a function of the argument x, then it is called periodic if there is a number T such that for any x F(x + T) = F(x). This number T is called period of the function.
Periods can be several. For example, the function F = const for all values of the argument takes the same value, and therefore any number can be considered as its period.
Usually the least interested in mathematics is not equal to zero the period of the function. It for the sake of brevity call just period.
Periods can be several. For example, the function F = const for all values of the argument takes the same value, and therefore any number can be considered as its period.
Usually the least interested in mathematics is not equal to zero the period of the function. It for the sake of brevity call just period.
2
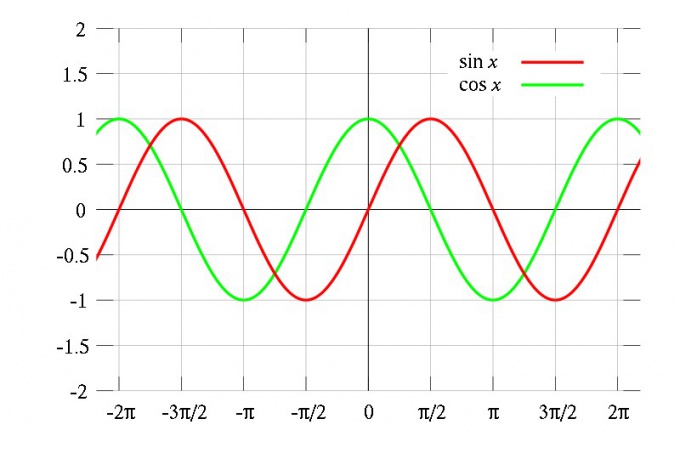
A classic example of periodic functions — trigonometric: sine, cosine, and tangent. Their period is the same and equal to 2π, i.e. sin(x) = sin(x + 2π) = sin(x + 4π), and so on. But, of course, trigonometric functions are not the only periodic.
3
Relatively simple, basic function the only way to establish their periodicity or periodical calculations. But for complex functions already have a few simple rules.
4
If F(x) is a periodic function with period T, and the derivative that the derivative f(x) = F'(x) is also periodic function with the period T. Because the value of the derivative at the point x equals the tangent of the angle of inclination of the tangent of the graph of its integral at this point to the x-axis, and since the integral is repeated periodically, it should be unique, and derivative. For example, the derivative of the function sin(x) equals cos(x) and it is periodic. Taking the derivative of cos(x) you get –sin(x). The frequency remains unchanged.
However, the reverse is not always true. So, the function f(x) = const periodic, but its integral F(x) = const*x + C no.
However, the reverse is not always true. So, the function f(x) = const periodic, but its integral F(x) = const*x + C no.
5
If F(x) is a periodic function with period T, then G(x) = a*F(kx + b), where a, b, and k are constants and k is not equal to zero — is also a periodic function and its period is T/k. For example sin(2x) is a periodic function and its period is π. Visually it can be represented as follows: multiplying x by some number, as if you compress the graph of horizontally in so many times
6
If F1(x) and F2(x) periodic functions and their periods are equal to T1 and T2 respectively, then the sum of these functions also can be periodic. However, her period is simply the sum of the periods T1 and T2. If the result of dividing the T1/T2 is a rational number, then the sum of the functions is periodic, and its period is the least common multiple (LCM) of the periods T1 and T2. For example, if the first function is equal to 12, and the period the second 15, the period of their sum will be equal to the NOC (12, 15) = 60.
Visually it can be represented as follows: the functions are with different "width of step", but if the ratio of their widths rationally, sooner or later (or rather, it is through the NOC steps), they are again equal, and their sum will start a new period.
Visually it can be represented as follows: the functions are with different "width of step", but if the ratio of their widths rationally, sooner or later (or rather, it is through the NOC steps), they are again equal, and their sum will start a new period.
7
However, if the ratio of the periods is irrational, then the total function is not periodic at all. For example, let F1(x) = x mod 2 (the remainder of dividing x by 2), and F2(x) = sin(x). Here T1 is 2, T2 is equal to 2π. The ratio of the periods is equal to π — an irrational number. Hence, the function sin(x) + x mod 2 is not periodic.