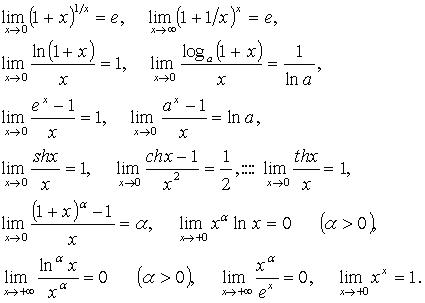Instruction
1
In mathematical analysis there is the concept of limits of sequences and functions. When you want to find the limit of a sequence, write it down in the following way: lim xn=a. In this sequence, the sequence xn tends to a, as n approaches infinity. The sequence is usually represented in the form of a number, for example:
x1, x2, x3...,xm,...,xn... .
Sequences are divided into ascending and descending. For example:
xn=n^2 is an increasing sequence of
yn=1/n is decreasing sequence
For example, the limit of the sequence xn=1/n^2 is equal to:
lim 1/n^2=0
x→∞
This limit is equal to zero, as n→∞, and the sequence 1/n^2 tends to zero.
x1, x2, x3...,xm,...,xn... .
Sequences are divided into ascending and descending. For example:
xn=n^2 is an increasing sequence of
yn=1/n is decreasing sequence
For example, the limit of the sequence xn=1/n^2 is equal to:
lim 1/n^2=0
x→∞
This limit is equal to zero, as n→∞, and the sequence 1/n^2 tends to zero.
2
Typically, a variable x tends to a finite limit a, and x continually approaches a and the value of a constant. Write it down as follows: limx =a, thus, n can also strive both to zero and to infinity. There are endless options, they limit tends to infinity. In other cases, for example, when a function describes a slowing down of the train, you can talk about the limit tends to zero.
Have limits there are a number of properties. As a rule, any function has only one limit. This is the main property of the limit. Other properties thereof are listed below:
* The limit of the sum is equal to the sum of the limits:
lim(x+y)=lim x+lim y
* The limit of a product is the product of the limits:
lim(xy)=lim x*lim y
* Limit the private equal to the quotient of:
lim(x/y)=lim x/lim y
* Constant multiplier take out the limit sign:
lim(Cx)=C lim x
If given the function 1 /x where x →∞, its limit is zero. If x→0, the limit of such function is equal to ∞.
For trigonometric functions, there are exceptions to these rules. Since the function sin x is always close to one when approaches zero, for her true identity:
lim sin x/x=1
x→0
Have limits there are a number of properties. As a rule, any function has only one limit. This is the main property of the limit. Other properties thereof are listed below:
* The limit of the sum is equal to the sum of the limits:
lim(x+y)=lim x+lim y
* The limit of a product is the product of the limits:
lim(xy)=lim x*lim y
* Limit the private equal to the quotient of:
lim(x/y)=lim x/lim y
* Constant multiplier take out the limit sign:
lim(Cx)=C lim x
If given the function 1 /x where x →∞, its limit is zero. If x→0, the limit of such function is equal to ∞.
For trigonometric functions, there are exceptions to these rules. Since the function sin x is always close to one when approaches zero, for her true identity:
lim sin x/x=1
x→0
3
In some tasks there are functions in the calculation of limits where there is uncertainty - a situation where the limit cannot be calculated. The only way out of this situation is the use of l'hospital's rule. There are two types of uncertainties:
* the uncertainty of 0/0
* the uncertainty of the form ∞/∞
For example, given the following limit: lim f(x)/l(x), and f(x0)=l(x0)=0. In this case, there is the uncertainty of 0/0. To solve this problem, both the function subjected to differentiation, and then find the limit of the result. Uncertainties of the kind 0/0, the limit is equal to:
lim f(x)/l(x)=lim f'(x)/l'(x) (with x→0)
The same is true for the indeterminate of type ∞/∞. But in this case, fairly following equality: f(x)=l(x)=∞
Using l'hospital's rule it is possible to find values for any limits, which involve uncertainty. A necessary condition for
Tom - no errors in finding the derivatives. For example, the derivative of the function (x^2)' is equal to 2x. From this we can conclude that:
f'(x)=nx^(n-1)
* the uncertainty of 0/0
* the uncertainty of the form ∞/∞
For example, given the following limit: lim f(x)/l(x), and f(x0)=l(x0)=0. In this case, there is the uncertainty of 0/0. To solve this problem, both the function subjected to differentiation, and then find the limit of the result. Uncertainties of the kind 0/0, the limit is equal to:
lim f(x)/l(x)=lim f'(x)/l'(x) (with x→0)
The same is true for the indeterminate of type ∞/∞. But in this case, fairly following equality: f(x)=l(x)=∞
Using l'hospital's rule it is possible to find values for any limits, which involve uncertainty. A necessary condition for
Tom - no errors in finding the derivatives. For example, the derivative of the function (x^2)' is equal to 2x. From this we can conclude that:
f'(x)=nx^(n-1)
Useful advice
An example of the problem of finding the limit by l'hospital's rule.
Given the following expression:
lim(1-cosx)/x^2
x →0
Since cosx=1, the uncertainty of the type 0/0.
The first derivative is equal to:
{(1-cosx)/x^2}'=sinx/2x
lim sinx/2x=0/0
x →0
From the last expression it is seen that the uncertainty arose again, so you need to take second derivative of this function:
{(sinx)/2x}'=cosx/2
Now the limit is equal to:
lim cosx/2=1/2
x→0
Answer: lim(1-cosx)/x^2=1/2
x→0
Given the following expression:
lim(1-cosx)/x^2
x →0
Since cosx=1, the uncertainty of the type 0/0.
The first derivative is equal to:
{(1-cosx)/x^2}'=sinx/2x
lim sinx/2x=0/0
x →0
From the last expression it is seen that the uncertainty arose again, so you need to take second derivative of this function:
{(sinx)/2x}'=cosx/2
Now the limit is equal to:
lim cosx/2=1/2
x→0
Answer: lim(1-cosx)/x^2=1/2
x→0