Instruction
1
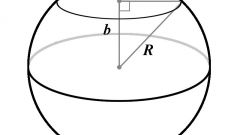
Given the scope and the known area of its surface. Then, using the formula to calculate the surface area of the sphere, we can calculate its radius:
R = v(4•P/S), where S is the surface area of the sphere, P = 3,14.
R = v(4•P/S), where S is the surface area of the sphere, P = 3,14.
2
If you know the volume of a sphere, which limits the sphere, the radius can be found by the formula:
R = (3•V/4•N)^1/3, where V is the volume of a sphere, P = 3,14.
R = (3•V/4•N)^1/3, where V is the volume of a sphere, P = 3,14.
Useful advice
In cases where the area of the inscribed or circumscribed about a regular polyhedron, you can use the following formulas.
For a sphere inscribed in a regular tetrahedron R = √6/12•a, where a is the edge length of a tetrahedron
For the sphere, described about a regular tetrahedron R = √6/4•a, where a is the edge length of a tetrahedron
For a sphere inscribed in a cube R = 1/2•a, where a is the edge length of the cube
For the sphere described about Cuba R = √3/2•a, where a is the edge length of the cube.
For a sphere inscribed in a regular tetrahedron R = √6/12•a, where a is the edge length of a tetrahedron
For the sphere, described about a regular tetrahedron R = √6/4•a, where a is the edge length of a tetrahedron
For a sphere inscribed in a cube R = 1/2•a, where a is the edge length of the cube
For the sphere described about Cuba R = √3/2•a, where a is the edge length of the cube.