How to find the cross-sectional area of the ball

Obviously, if the distance from the center of the sphere to the plane is equal to the radius of the plane, the plane touches the globe at one point only, and the cross-sectional area will be equal to zero, i.e. if b = R then S = 0. If b = 0, then the secant plane passes through the center of the ball. In this case, the cross section will be a circle, whose radius coincides with the radius of the ball. The area of this circle will, according to the formula, equal to S = NR^2.

These two extreme cases provide the boundaries between which will always be based on the required area: 0 < S < NR^2. Thus any section of the sphere with a plane is always a circle. Consequently, the task is to find the radius of circumference section. Then the area of this cross section is calculated according to the formula of circle area.

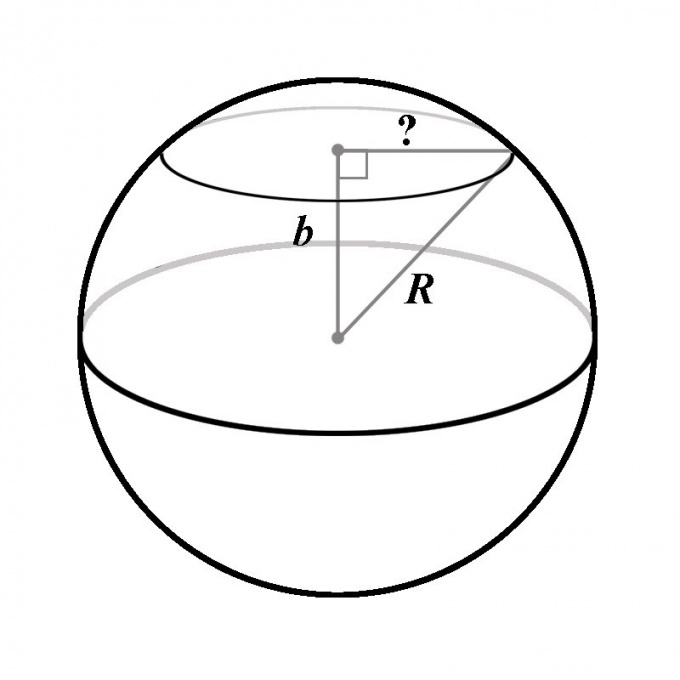
As the distance from the point to the plane is defined as the length of the segment perpendicular to the plane and starts at the point, the second end of this segment coincides with the center of the circle section. This conclusion follows from the definition of a ball: it is obvious that all points of the circumference of the section belong to the field, and therefore lie at an equal distance from the center of the ball. This means that each point on the circumference of the cross section can be considered as the vertex of a right triangle, the hypotenuse is the radius of the ball, one of the legs is perpendicular to the segment connecting the center of the ball with the plane, and the second leg — the radius of the circle cross section.

Of the three sides of this triangle contains two — the radius of the ball R and the distance b, that is the hypotenuse and a leg. By the Pythagorean theorem the length of the second leg should be equal to √(R^2 - b^2). This is the radius of the circle cross section. Substituting the found value of the radius in the formula for the area of a circle, it is easy to conclude that the cross-sectional area of the sphere with a plane is equal to:S = π(R^2 - b^2).In the special case when b = R or b = 0, the derived formula is completely consistent with the already found results.