Instruction
1
If you know the circumference (L), its radius (r) will be determined by the ratio of the circumference to twice the number PI: r=L/(2∗π). For example, if we know the circumference is five meters, the radius can be defined as: 5/(2∗3,14) = 5/6,28 = 79,62 cm.
2
If you know the area of a circle (S), radius (r) can be defined as the square root of the area ratio and the number PI: r=√(S/π). For example, if the area of a circle is five square meters, the radius can be calculated as: √(5/3,14) = √1,59 = 1,26 meters.
3
If you know the lengths of the sides (a and b) inscribed in a circle of rectangle, radius of circle (r) will be determined as half the diagonal of this rectangle. And since the diagonal length according to the Pythagorean theorem, we can assume the square root of the sum of the lengths of the sides squared, the radius is equal to half of this value: r=0.5∗√(a2 + b2). For example, if the lengths of the known sides equal to two and four meters, the length of the radius can be defined as: 0.5∗√(22 + 42) = 0.5∗√20 = 0.5∗4.47 = 2,24 meters.
4
Practical calculations can be produced, for example, the standard calculator of Windows operating system. The link to the run is placed in one of the subsections of the main menu on the "start" button. Opening it, click All programs, click Accessories, then select system tools and finally, the item "Calculator". An alternative method is to use the run dialog programs that opens by pressing the key combination WIN + R. In this dialogue you can enter the command calc and click the "OK"button.
Note
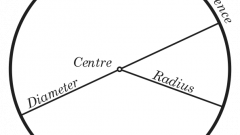
How to find the radius of the circle? Guénon convenient search of answers to questions. Circle — a closed plane curve, all points of which are equidistant from a given point (center) lying in the same plane as the curve. Circle the part of the plane bounded by a circle. Radius — line segment connecting the center of the circle with any point as well as the length of this segment.
Useful advice
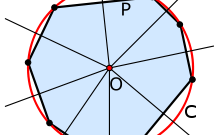
Depending on the conditions of the problem the radius of the circle you can find. Formula 1: R = L / 2π where L is the length of the circle, and π is a constant equal to 3,141 Formula 2: R = √( S / π), where S is the magnitude of the area of a circle. How to find the radius of the circumscribed circle. First, let's define the term itself. The circle described is called when it touches all vertices of the given polygon.