You will need
- The triangle with the given parameters
- The compass
- Line
- Gon
- Table of sines and cosines
- Mathematical concepts
- Determination of the height of the triangle
- Formulas of sines and cosines
- Formula of area of triangle
Instruction
1
Draw a triangle with the desired settings. The triangle can be build either on three sides or by two sides and angle between them, or a side and two adjacent angles thereto. Label the vertices of the triangle as A, b and C, the angles as α, β, and γ, and opposite the vertex angle side as a, b and c.
2
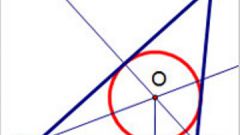
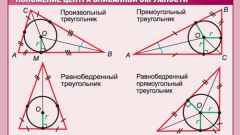
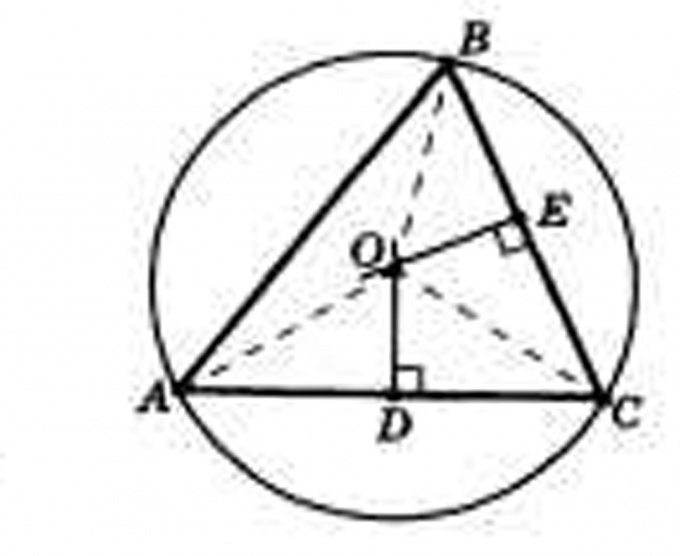
Guide height to all sides of the triangle and find the point of intersection. Label the height as h with the corresponding sides of indices. Find the point of intersection and label it O. She will be the center of the circle. Thus, the radius of this circle will be the segments OA, Ob and OC.
3
The radius of the circumscribed circle can be found in two formulas. For one you must first calculate the area of a triangle. It is equal to the product of all the sides of a triangle the sine of any of the angles divided by 2.
S=abc*sinα
In this case, the radius of the circumscribed circle is calculated by the formula
R=a*b*c/4S
For other formulas, it is sufficient to know the length of one side and the sine of its opposite angle.
R=a/2sinα
Calculate the radius and describe a triangle around the circumference.
S=abc*sinα
In this case, the radius of the circumscribed circle is calculated by the formula
R=a*b*c/4S
For other formulas, it is sufficient to know the length of one side and the sine of its opposite angle.
R=a/2sinα
Calculate the radius and describe a triangle around the circumference.
Useful advice
Remember, what is the height of the triangle. It is the perpendicular drawn from angle to opposite side.
The area of a triangle can be represented as the product of the square of one of the parties to the sines of the two adjacent angles, divided by the doubled sine of the sum of these angles.
S=A2*sinβ*sinγ/2sinγ
The area of a triangle can be represented as the product of the square of one of the parties to the sines of the two adjacent angles, divided by the doubled sine of the sum of these angles.
S=A2*sinβ*sinγ/2sinγ