Instruction
1
If you are aware of the volume V and the height of the cone H, we can Express the radius of the base R from the formula V=1/3∙πR2H. Get: R2=3V/πH, where R=√(3V/πH).
2
If you know the lateral surface area of the cone S and the length of its generatrix L, Express the radius R from the formula: S=πRL. You will get R=S/πL.
3
The following ways of finding the radius of the base of the cone based on the assertion that the cone formed by rotating a right triangle around one of the legs to the axle. So, if you are aware of the height of the cone H and the length of its generatrix L, that to find the radius R you can use the Pythagorean theorem: L2=R2+H2. Express this formula R, we get: R2=L2–H2, and R=√(L2–H2).
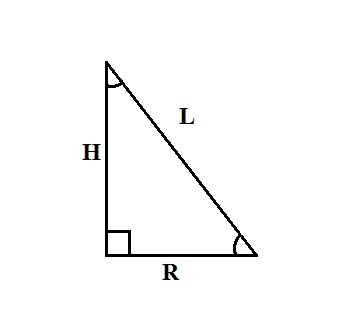
4
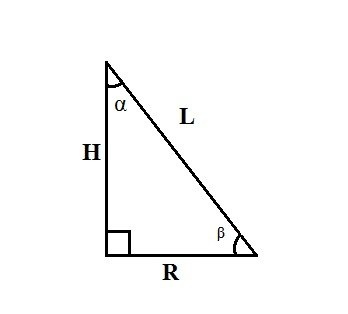
Use the rules of the relationships between the sides and angles in a right triangle. If you know the forming of the cone L and the angle α between the height of the cone and its generating line, find the base radius R, equal to one of the legs of a right triangle, using the formula: R=L∙sinα.
5
If you know the forming of the cone L and the angle β between the base radius of the cone and its generating line, find the base radius R by the formula: R=L∙cosβ. If you know the height of the cone H and the angle α between the generatrix and the radius of the base, find the base radius R by the formula: R=H∙tgα.
6
Example: forming of a cone L is 20 cm and the angle α between the generatrix and cone height equal to 15º. Find the base radius of the cone. Solution: In a right triangle with hypotenuse L and an acute angle α opposite the side angle R is calculated by formula R=L∙sinα. Substitute the corresponding values, we get: R=L∙sinα=20∙sin15º. Sin15º is from formulas of trigonometric functions of half argument and equal to 0.5√(2–√3). Hence the leg R=20∙0,5√(2–√3)=10√(2–√3)see, Respectively, the base radius of the cone R is equal to 10√(2–√3)cm.
7
A special case: in a right triangle the side opposite the 30º angle is half the hypotenuse. Thus, if we know the length of the generatrix of the cone and the angle between its generatrix and a height equal to 30º, then find the radius using the formula: R=1/2L.


