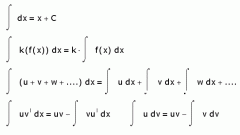Instruction
1
As a rule, the evaluation of the integral boils down to, to bring the integrand to the tabular view. There are many table-valued integrals, which facilitates the solution of such problems.
2
There are several ways to bring the integral to a convenient form: direct integration, integration by parts, the substitution method, the introduction under the sign of the differential, the Weierstrass substitution, etc.
3
The method of direct integration is the successive reduction of the integral to the tabular view by using elementary transformations:∫соѕ2 (x/2)DX = 1/2•∫(1 + cos x)DX = 1/2•∫DX + 1/2•∫cos xdх = 1/2•(x + sin x) + C, where C is a constant.
4
Integral has many possible values based on the properties of the integral, namely the presence of summable constants. Thus, it was found in the sample solution is shared. The private solution of the integral is called the total at a certain constant value, for example, With=0.
5
Integration by parts is used when the integrand is a product of algebraic and transcendental functions. The method formula:∫udv = u•v - ∫vdu.
6
Because the position of the multipliers in the product do not matter, as the function u to choose one part of the expression, which after differentiation is simplified. Example:∫x·ln xdx = [u=ln x; v=x; dv=xdx] = x2/2·ln x – ∫x2/2·dx/x = x2/2·ln x – x2/4 + C.
7
The introduction of the new variable is a technique for method lookup. This changes and she integrand, and its argument:∫x·√(x - 2)dx = [t=x-2 → x = t2+2 → dx=2·tdt] = ∫(t2 + 2)·t·2·tdt = ∫(2·t^4 + 4·t2)dt = 2·t^5/5 + 4·t3/3 + C = [x=t2+2] = 2/5·(x - 2)^(5/2) + 4/3·(x - 2)^(3/2) + C.
8
Method of introducing, under the sign of the differential involves the transition to new functions. Let ∫f(x) = F(x) + C and u = g(x), then ∫f(u)du = F(u) + C [g’(x) = dg(x)]. Example:∫(2·x + 3)2dx = [dx = 1/2·d(2·x + 3)] = 1/2·∫(2·x + 3)2d(2·x + 3) = 1/6·(2·x + 3)3 + C.