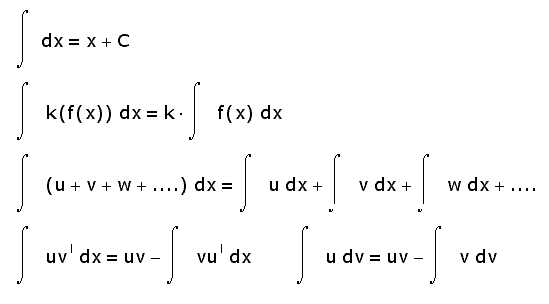Instruction
1
Imagine some function F(x), the derivative of which is f(x). This expression can be written in the following form:
F'(x)=f(x).
If the function f(x) is the derivative of the function F(x), the function F(x) is a primitive for f(x).
The same function can be somewhat primitive. An example of this might be a function x^2. It has an infinite number of primitives, among them major - such as x^3/3 or x^3/3+1. Instead of the units or any other number specified constant C, which is written as follows:
F(x)=x^n+C, where C=const.
The integration is called finding the integral of the function, inverse of the differential. The integral denoted by the sign ∫. It can be as vague, when given some function with an arbitrary C, and particular when it has some value. In this case, the integral is given by two values, called upper and lower limits.
F'(x)=f(x).
If the function f(x) is the derivative of the function F(x), the function F(x) is a primitive for f(x).
The same function can be somewhat primitive. An example of this might be a function x^2. It has an infinite number of primitives, among them major - such as x^3/3 or x^3/3+1. Instead of the units or any other number specified constant C, which is written as follows:
F(x)=x^n+C, where C=const.
The integration is called finding the integral of the function, inverse of the differential. The integral denoted by the sign ∫. It can be as vague, when given some function with an arbitrary C, and particular when it has some value. In this case, the integral is given by two values, called upper and lower limits.
2
Since the integral is an inverse value of the derivative in a General form it looks like this:
∫f(x)=F(x)+C.
For example, using a table of differentials, it is possible to find the integral of the function y=cosx:
∫cosx=sinx as the derivative of the function f(x) equal to f'(x)=(sinx)'=cosx.
The integrals there are other properties. Listed below are only the most basic of them:
- integral of the sum is equal to the sum of the integrals;
- the constant factor can be removed from the integral sign;
∫f(x)=F(x)+C.
For example, using a table of differentials, it is possible to find the integral of the function y=cosx:
∫cosx=sinx as the derivative of the function f(x) equal to f'(x)=(sinx)'=cosx.
The integrals there are other properties. Listed below are only the most basic of them:
- integral of the sum is equal to the sum of the integrals;
- the constant factor can be removed from the integral sign;
3
In some problems, especially in geometry and physics, applied integrals of another type - specific. For example, it can be used if necessary to determine the distance, which was a material point between time periods t1 and t2.
4
There are technical devices capable of integration. The simplest of them - integrating analog chain. It is available in integrating voltmeters, and in some of the dosimeters. Later was invented the digital integrators - pulse counters. Currently, the function of integrator you can assign software to any device that has a microprocessor.