Instruction
1
When graphing two given functions in the area of their intersection is formed a closed figure bounded by these curves and two straight lines x=a and x=b, where a and b are the ends of the considered interval. This figure visually displays the touch. Its area can be calculated proindeksirovat difference functions.
2
Feature located above on the chart, is the larger value, hence the formula of its expression will be the first: S = ∫f1 ∫f2, where f1 > f2 on the interval [a, b]. However, taking into account that the quantitative characteristic of any geometric object is a positive value, we can calculate the area of the figure bounded the graphs of the functions in the module:
S = |∫f1 ∫f2|.
S = |∫f1 ∫f2|.
3
This option is especially useful if there is no opportunity or time to build the graph. When calculating a definite integral you use the rule of the Newton-Leibniz, which involves the substitution in the final result the limit values of the interval. Then the area of the shape equal to the difference between two values of the integral found at the integration phase, of greater F(b) and the smaller F(a).
4
Sometimes a closed figure on a given interval is formed by the complete intersection of the graphs of functions, i.e., the endpoints of the interval are points that belong to both curves. Example: find the points of intersection of the lines y = x/2 + 5 and y = 3•x – x2/4 + 3 and calculate the area.
5
Solution.
To find the intersection points, write down the equation:
x/2 + 5 = 3•x – x2/4 + 3 → x2 – 10•x + 8 = 0
D = 100 - 64 = 36 → x1,2 = (10 ± 6)/2.
To find the intersection points, write down the equation:
x/2 + 5 = 3•x – x2/4 + 3 → x2 – 10•x + 8 = 0
D = 100 - 64 = 36 → x1,2 = (10 ± 6)/2.
6
So you've found the ends of the interval of integration is [2; 8]:
S = |∫ (3•x – x2/4 + 3 – x/2 - 5)DX| = |(5•x2/4 – X3/12 - 2•x)| ≈ 59.
S = |∫ (3•x – x2/4 + 3 – x/2 - 5)DX| = |(5•x2/4 – X3/12 - 2•x)| ≈ 59.
7
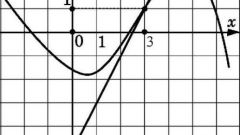
Consider another example: U1 = √(4•x + 5); Y2 = x and the equation of the line x = 3.
In this task, only one end of the interval x=3. This means that the second value you want to find the schedule. Construct a line defined by the functions U1 and U2. It is obvious that the value x=3 is the upper limit, therefore, need to determine the lower limit. For this Paranaita expression:
√(4•x + 5) = x ↑2
4•x + 5 = x2 → x2 – 4•x – 5 = 0
In this task, only one end of the interval x=3. This means that the second value you want to find the schedule. Construct a line defined by the functions U1 and U2. It is obvious that the value x=3 is the upper limit, therefore, need to determine the lower limit. For this Paranaita expression:
√(4•x + 5) = x ↑2
4•x + 5 = x2 → x2 – 4•x – 5 = 0
8
Find the roots of the equation:
D = 16 + 20 = 36 → x1 = 5; x2 = -1.
Look at the chart, the lower interval value is -1. Since U1 is above U2, then:
S = ∫(√(4•x + 5) - x)DX on the interval [-1; 3].
S = (1/3•√((4•x + 5)3) – x2/2) = 19.
D = 16 + 20 = 36 → x1 = 5; x2 = -1.
Look at the chart, the lower interval value is -1. Since U1 is above U2, then:
S = ∫(√(4•x + 5) - x)DX on the interval [-1; 3].
S = (1/3•√((4•x + 5)3) – x2/2) = 19.