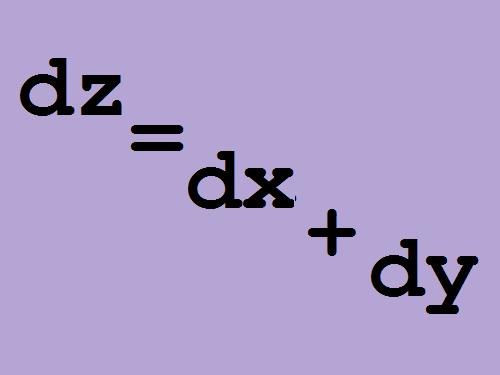Instruction
1
Differential (from lat. "the difference") is the linear part of the full increment function. Differential denoted by df, where f is a function. The function of a single argument is sometimes portrayed dxf or dxF. Suppose there is a function z = f(x, y), a function of two arguments x and y. Then the total increment of the function will be:
f(x, y) – f(x_0, y_0) = f _x (x, y)*(x – x_0) + f _y(x ,y)*(y – y_0) + α, where α is infinitesimal (α → 0), which is ignored in the definition of the derivative as lim α = 0.
f(x, y) – f(x_0, y_0) = f _x (x, y)*(x – x_0) + f _y(x ,y)*(y – y_0) + α, where α is infinitesimal (α → 0), which is ignored in the definition of the derivative as lim α = 0.
2
Differential of function f for argument x is a linear function of relative increment (x – x_0), i.e. df(x_0) = f _x_0 (Δx).
3
Geometrical meaning of the differential of a function: if a function f is differentiable at x_0, then its differential at this point is the increment of the ordinate (y) a tangent line to the graph of the function.
The geometric meaning of the total differential of a function of two arguments is three – dimensional analogue of the geometric meaning of the differential of a function of one argument, i.e. that the increment of applicati (z) the tangent plane to the surface whose equation is set to a differentiable function.
The geometric meaning of the total differential of a function of two arguments is three – dimensional analogue of the geometric meaning of the differential of a function of one argument, i.e. that the increment of applicati (z) the tangent plane to the surface whose equation is set to a differentiable function.
4
You can write the total differential of a function using the increment function and arguments is a more common form of entry:
Δz = (δz/δx)dx + (δz/δy)dy, where δz/δx is the derivative of the function z for the argument x, δz/δy is the derivative of the function z for the y argument.
Say that a function f(x, y) differentiable at (x, y), if such x and y values you can define the total differential of this function.
The expression (δz/δx)dx + (δz/δy)dy is the linear part of the increment of the original function, where (δz/δx)dx is the differential of a function z on x, and (δz/δy)dy the differential of y. While differentiation according to one of the arguments assume that the other argument or arguments (if several) - constant values.
Δz = (δz/δx)dx + (δz/δy)dy, where δz/δx is the derivative of the function z for the argument x, δz/δy is the derivative of the function z for the y argument.
Say that a function f(x, y) differentiable at (x, y), if such x and y values you can define the total differential of this function.
The expression (δz/δx)dx + (δz/δy)dy is the linear part of the increment of the original function, where (δz/δx)dx is the differential of a function z on x, and (δz/δy)dy the differential of y. While differentiation according to one of the arguments assume that the other argument or arguments (if several) - constant values.
5
Example.
Find the total differential of the following function: z = 7*x^2 + 12*y - 5*x^2*y^2.
Solution.
Using the assumption that y is a constant, find the partial derivative in the argument x,
δz/δx = (7*x^2 + 12*y - 5*x^2*y^2)’dx = 7*2*x + 0 – 5*2*x*y^2 = 14*x – 10*x*y^2;
Using the assumption that x is a constant, find the partial derivative for the y argument:
δz/δy = (7*x^2 + 12*y - 5*x^2*y^2)’dy = 0 + 12 – 5*2*x^2*y = 12 – 10x^2*y.
Find the total differential of the following function: z = 7*x^2 + 12*y - 5*x^2*y^2.
Solution.
Using the assumption that y is a constant, find the partial derivative in the argument x,
δz/δx = (7*x^2 + 12*y - 5*x^2*y^2)’dx = 7*2*x + 0 – 5*2*x*y^2 = 14*x – 10*x*y^2;
Using the assumption that x is a constant, find the partial derivative for the y argument:
δz/δy = (7*x^2 + 12*y - 5*x^2*y^2)’dy = 0 + 12 – 5*2*x^2*y = 12 – 10x^2*y.
6
Write down the total differential of a function:
dz = (δz/δx)dx + (δz/δy)dy = (14*x – 10*x*y^2)dx + (12 – 10x^2*y).
dz = (δz/δx)dx + (δz/δy)dy = (14*x – 10*x*y^2)dx + (12 – 10x^2*y).
Note
At some point the function can be defined by the partial derivatives according to one of the arguments, but the differential may not exist for the combination of these values.