Instruction
1
For the square perimeter (P) is equal to four times the value of one side (b). P = 4*b or the sum of the lengths of all sides P = b + b + b + b. The area of a square is expressed as the product of two adjacent sides. Find the length of one side of the square. If you only know the area (S), remove its value the square root a = √S. Then determine the perimeter.
2
Given: area of square is 36 cm2. Find the perimeter of a figure.Solution 1. Find the side of squareb = √S, b = √36 cm2, b =6 cm, Find the perimeter: P = 4*b, P = 4*6cm, P = 24 cm P = 6 + 6 + 6 + 6 R = 24cm.Answer: the perimeter of a square with an area of 36 cm2 24 cm
3
To find the perimeter of the square through the square without extra action (computation). Use the formula for perimeter is valid only for square P = 4*√S.
4
Solution 2. Find the perimeter of a square: P = 4*√S, P = 4*√36см2, P = 24 cm Answer: perimeter of square is 24 cm
5
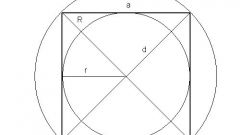
Many of the parameters of this geometric shape are linked. Knowing one of them, you'll be able to find any other. There are also the following calculation formula:Diagonal: a2 = 2*b2, where a is the diagonal, b – side of the square. Or a2=2S.The radius of the inscribed circle: r = b/2 where b – side.Radius of circumscribed circle: R = ½*d, where d is the diagonal of the square.The diameter of the circumcircle: D = f, where f is diagonal.
Note
The beneficial properties of a square:
A square is regular quadrilateral, having the properties of a rectangle and a rhombus.
Square – a rectangle where all sides are equal.
The square – rhombus in which all angles are at 90 degrees.
A square face of the cube.
The diagonals of a square are equal and intersect at right angles.
The diagonal of a square divides it into two equal right triangle and is the hypotenuse for each of these triangles.
The diagonal of a square is the diameter described in the shape of a circle.
A square is regular quadrilateral, having the properties of a rectangle and a rhombus.
Square – a rectangle where all sides are equal.
The square – rhombus in which all angles are at 90 degrees.
A square face of the cube.
The diagonals of a square are equal and intersect at right angles.
The diagonal of a square divides it into two equal right triangle and is the hypotenuse for each of these triangles.
The diagonal of a square is the diameter described in the shape of a circle.