Instruction
1
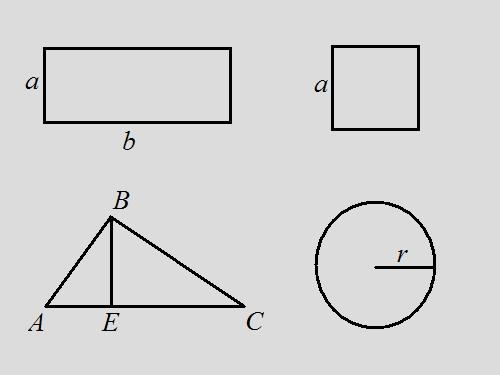
Prjamougolnosti: find the perimeter of a rectangle if you know that the area is equal to 18, and the length of a rectangle is 2 times the width.Solution: write the formula for area of a rectangle S = a*b. The statement b = 2*a, hence 18 = a*2*a, a = √9 = 3. It is obvious that b = 6. According to the formula the perimeter is equal to the sum of all the sides of the rectangle P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18. In this problem the perimeter is matched by value with the area of the figure.
2
Quadratscha: find the perimeter of a square if its area is 9.Solution: by formula the area of a square S = a^2, hence find the length of side a = 3. The perimeter is equal to the sum of the lengths of all sides hence P = 4*a = 4*3 = 12.
3
Treugolnika: given an arbitrary triangle ABC, the square of which is equal to 14. Find the perimeter of a triangle, if drawn from the vertex B, the altitude divides the base of the triangle into segments of length 3 and 4, see the Solution: by formula the area of a triangle is half the work of the Foundation to the height, i.e., S = ½*AC*BE. The perimeter is equal to the sum of the lengths of all sides. The length of the side AC find the folding of the lengths AE and EC, AC = 3 + 4 = 7. Find the height of the triangle BE = S*2/AC = 14*2/7 = 4.Consider the right triangle ABE. Knowing the legs AE and BE, we can find the hypotenuse by the formula of Pythagoras, AB^2 = AE^2 + BE^2, AB = √(3^2 + 4^2) = √25 = 5.Consider the right triangle BEC. By the formula of Pythagoras BC^2 = BE^2 + EC^2, BC = √(4^2 + 4^2) = 4*√2.Now known the lengths of all sides of the triangle. Find the perimeter of their sum P = AB + BC + AC = 5 + 4*√2 + 7 = 12 + 4*√2 = 4*(3+√2).
4
Ukrainetoday: it is known that the area of the circle is 16*PI, find its perimeter.Solution: write the formula for area of a circle S = π*r^2. Find the radius of the circle r = √(S/π) = √16 = 4. According to the formula of the perimeter P = 2*π*r = 2*π*4 = 8*π. If we assume that π = 3.14, P = 8*3.14 = 25.12.