How to find side of a square if you know its area

To find side of a square if you know its area, remove from the numeric value of the square of the square root. That is, find a number, square (second degree) which is equal to the area of a square. As a formula this rule is written as follows:a = √S, where a is the side length of the square
S – the area of a square.The length of a side of a square is measured in corresponding linear units. For example, if the area of a square is 16 square centimeters (cm2), the length of its side will be equal to 4 centimeters (cm).

To calculate the square root of the number, take the calculator (this is where the notation of mathematical functions). Type on the keyboard of the calculator the numerical value of the area of a square. Then click on the button marked as "√". The numerical value of the length of a side of a square will appear on the display of the calculator.

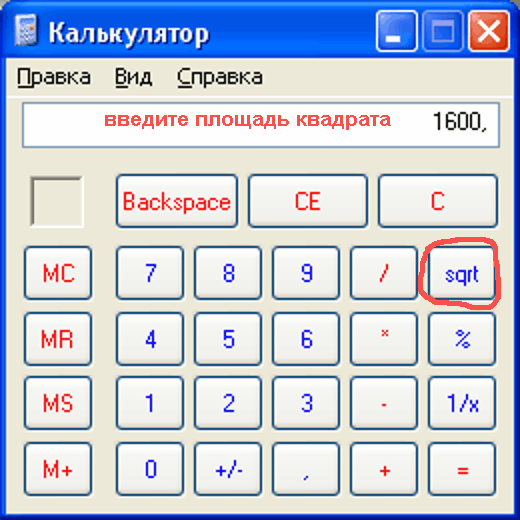
To calculate the square root on the computer, start the standard Windows calculator. Switch it to "normal" (not engineering!) . Then type the area value. Click on the button labeled as "sqrt".

To find side of a square with a given area you can use the program MS Excel. To do this, run the program Excel, put the cursor on any cell and click "=". Then click on this icon select the function (fx) Select from the list the function "ROOT". Then type in the window opened, the numeric value of the area of a square, and then click OK (or press Enter). The value of the square root, and thus the length of a side of a square then appears in the cell.