Instruction
1
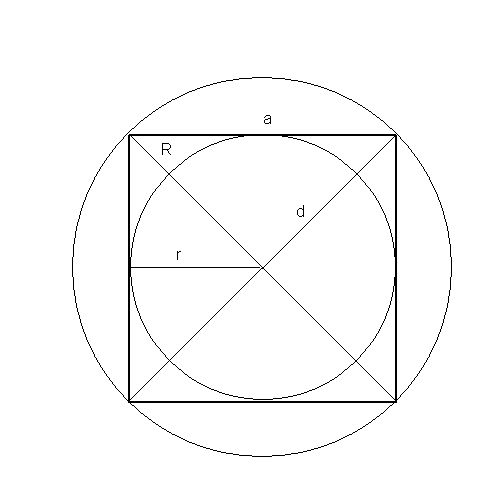
If you know the length of a side of the square, then its area is equal to the square (second degree) side.
Example 1.
Let us take a square with sides of 11 mm.
Determine its area.
Solution.
We denote by:
a - the length of a side of a square,
S – the area of a square.
Then:
S=a*a=A2=112=121 mm2
Answer: the Area of a square with sides of 11 mm – 121 mm2.
Example 1.
Let us take a square with sides of 11 mm.
Determine its area.
Solution.
We denote by:
a - the length of a side of a square,
S – the area of a square.
Then:
S=a*a=A2=112=121 mm2
Answer: the Area of a square with sides of 11 mm – 121 mm2.
2
If you know the perimeter of a square, then its area is equal to the sixteenth part of the square (second degree) of the perimeter.
Follows from the fact that all (four) sides of the square have the same length.
Example 2.
Suppose we have a square with a perimeter of 12 mm.
Determine its area.
Solution.
We denote by:
R - the perimeter of the square
S – the area of a square.
Then:
S=(P/4)2=P2/42=P2/16=122/16=144/16=9 mm2
Answer: the Area of a square with a perimeter of 12 mm 9 mm2.
Follows from the fact that all (four) sides of the square have the same length.
Example 2.
Suppose we have a square with a perimeter of 12 mm.
Determine its area.
Solution.
We denote by:
R - the perimeter of the square
S – the area of a square.
Then:
S=(P/4)2=P2/42=P2/16=122/16=144/16=9 mm2
Answer: the Area of a square with a perimeter of 12 mm 9 mm2.
3
If you know the radius of the inscribed square of the circle, its area is quadrupled (multiplied by 4) to the square (second degree) radius.
Follows from the fact that the radius of the inscribed circle is equal to half the length of the sides of a square.
Example 3.
Suppose we have a square with a radius of the inscribed circle 12 mm.
Determine its area.
Solution.
We denote by:
r is the radius of the inscribed circle,
S – the area of a square
a - the length of a side of a square.
Then:
S=A2=(2*r)=4*r2=4*122=4*144=576 mm2
Answer: the Area of a square with the radius of the inscribed circle 12 mm – 576 mm2.
Follows from the fact that the radius of the inscribed circle is equal to half the length of the sides of a square.
Example 3.
Suppose we have a square with a radius of the inscribed circle 12 mm.
Determine its area.
Solution.
We denote by:
r is the radius of the inscribed circle,
S – the area of a square
a - the length of a side of a square.
Then:
S=A2=(2*r)=4*r2=4*122=4*144=576 mm2
Answer: the Area of a square with the radius of the inscribed circle 12 mm – 576 mm2.
4
If you know the radius of a square circumscribed around a circle, then its area is equal to twice (multiplied by 2) to the square (second degree) radius.
Follows from the fact that the radius of the circumscribed circle is equal to half the diameter of the square.
Example 4.
Suppose you have a square with a circumscribed circle radius of 12 mm.
Determine its area.
Solution.
We denote by:
R is the radius of the circumscribed circle,
S – the area of a square
a - the length of a side of a square,
d – the diagonal of a square
Then:
S=A2=d2/2=(2R2)/2=2R2=2*122=2*144=288 mm2
Answer: the Area of a square with the radius of the circumscribed circle 12 mm – 288 mm2.
Follows from the fact that the radius of the circumscribed circle is equal to half the diameter of the square.
Example 4.
Suppose you have a square with a circumscribed circle radius of 12 mm.
Determine its area.
Solution.
We denote by:
R is the radius of the circumscribed circle,
S – the area of a square
a - the length of a side of a square,
d – the diagonal of a square
Then:
S=A2=d2/2=(2R2)/2=2R2=2*122=2*144=288 mm2
Answer: the Area of a square with the radius of the circumscribed circle 12 mm – 288 mm2.
5
If you know the diagonal of a square, then its area is half of the square (second degree) of the length of the diagonal.
It follows from the Pythagorean theorem.
Example 5.
Suppose we have a square with a diagonal length of 12 mm.
Determine its area.
Solution.
We denote by:
S – the area of a square
d – the diagonal of a square,
a - the length of a side of a square.
Then, since by the Pythagorean theorem: A2+A2=d2
S=A2=d2/2=122/2=144/2=72 mm2
Answer: the Area of a square with a diagonal of 12 mm to 72 mm2.
It follows from the Pythagorean theorem.
Example 5.
Suppose we have a square with a diagonal length of 12 mm.
Determine its area.
Solution.
We denote by:
S – the area of a square
d – the diagonal of a square,
a - the length of a side of a square.
Then, since by the Pythagorean theorem: A2+A2=d2
S=A2=d2/2=122/2=144/2=72 mm2
Answer: the Area of a square with a diagonal of 12 mm to 72 mm2.
Note
Denote side of the square as "b". By definition, area is product of length and width. The length of the square is equal to b, the width too. Therefore, the area of a square can be equated to the square of its sides: S=b2.
Useful advice
The area of a square is equal to the square of its side.