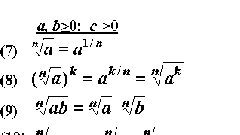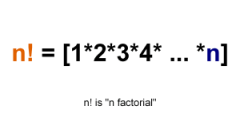How to put a negative number in degree

The operation of raising to a degree is binary, i.e. has two required input arguments and one output. One of the initial parameters is called the exponent determines the number of times that a multiplication operation needs to be applied to the second parameter - the base. The base can be both positive and negative numbers.

Instruction

Use the exponentiation of a negative number are common to the operation of the rule. As for positive integers, exponentiation means multiplying the original value by itself the number of times per unit less the exponent. For example, to build in the fourth degree, the number -2, it must three times to multiply by itself: -2⁴=-2*(-2)*(-2)*(-2)=16.

Multiplying two negative numbers always gives a positive value, and the result for values with different signs is negative. From this we can conclude that in the construction of negative values in the degree with even index should always be positive, and at odd indices of the result will always be less than zero. Use this property to check of the calculations. For example, the -2 in the fifth degree should be a negative number -2⁵=-2*(-2)*(-2)*(-2)*(-2)=-32, and -2 in the sixth, positive -2⁶=-2*(-2)*(-2)*(-2)*(-2)*(-2)=64.

During the construction of the negative of the power index can be given in the format of fractions, for example, -64 to degree⅔. This figure means that the original value be raised to the degree equal to the numerator, and extract the root degree equal to the denominator. One part of this operation, considered in the previous steps, but here you should pay attention to another.

The root is an odd function, that is, for negative real numbers it can only be used for odd exponent. Even if this feature does not matter. So, if you need to build a negative number to a fractional degree with an even denominator, then the problem has no solution. In all other cases, do the first transaction from the first two steps, using as the exponent of the numerator of the fraction, and then extract the root with the degree of the denominator.

Is the advice useful?