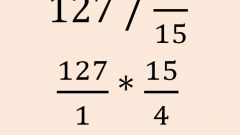How to represent number in the form fractions

If in the form of ordinary fractions must represent a whole number, use as the denominator of the unit and the original value put in the numerator. This form of recording will be called an ordinary improper fraction because its numerator more than the denominator module. For example, the number 74 can be recorded as 74/1, and the number -12 - as -12/1. If necessary, you can increase the numerator and denominator by the same percentage value of the fraction in this case will still match the original number. For example, 74=74/1=222/3 or -12=-12/1=-84/7.

If the original number is represented in decimal fraction, then its integer part to leave without change, and the separating comma, replace with a space. The fractional part is put in the numerator and in the denominator, use ten raised to the power with exponent equal to the number of digits in the fractional part of the original number. The resulting fractional part can be reduced, divide the numerator and the denominator by the same number. For example, the decimal fraction 7,625 would correspond to an ordinary fraction 625/1000 7, which after reduction will be set to 7 5/8. This form of entry common fraction is called mixed. If necessary, it can lead to incorrect ordinary mind, by multiplying the integer portion by the denominator and adding the result to the numerator: 7,625 = 7 625/1000 = 7 5/8 = 61/8.

If the original decimal is infinite and periodic, use, for example, the system of equations to calculate its equivalent in the format of fractions ordinary. For example, if the original fraction is equal to 3.5(3), it is possible to make such identity: 100*x-10*x=100*3,5(3)-10*3,5(3). From it we can deduce the equality 90*x=318, this means that the desired fraction is equal to 318/90 that the reduction will give a mixed common fraction 3 24/45.