How to count the degree

We are often faced with degrees in various fields of life and even in the home. When it comes to square meters or cubic, it is said, too, about the number in the second or third degree, when we see the marking very small or on the contrary big values, is often used 10^n. And, of course, there are many formulae involving degrees. And what actions are possible with degrees and how to count them?

Instruction

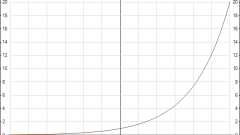
Let's start with the basics, with definitions. The degree is the product of equal factors. The multiplier is called the base, and the number of factors is the exponent. The action which is produced with the degree is called exponentiation.
The exponent can be positive or negative, integer or fraction, the following rules apply with degrees remain the same.
If the base of power is negative and the exponent is odd, then the result of exponentiation of a negative, but if the exponent is even, the result, regardless of whether negative or positive sign before the Foundation of the degree, will always have a plus sign.

All properties that we now enumerate, valid for powers with the same base. If the Foundation of the different degrees, then fold or subtracted after exponentiation. As well as multiply and divide. Because exponentiation, according to the established order of execution of arithmetic operations takes precedence over multiplication and division, and addition and subtraction, which are carried out in the last turn. Is this a strict sequence of actions, there are brackets, in which are the priority actions.

What are the special rules of arithmetic are there for degrees for about the same reason? Remember the following properties of exponents. If you see a product of two exponential expressions, for example a^n*a^m, then can be folded degree, so a^(n+m). Similarly, there are private, but the degree is already subtracted one from the other. a^n/a^m = a^(n-m).

In the case where the required erection in the degree other degree (a^n)^m, then the exponents are multiplied and we get a^(n*m).

The following important rule, if the base of power can be represented in the form of a product, we can convert the expression (a*b)^n a^n*b^n. Similarly, you can convert the fraction. (a/b)^n = a^n/b^n.

The final guidance. If the exponent zero, the result of the exponentiation will always be one. If the exponent is negative, that is a fractional expression. That is, a^-n = 1/a^n. And one last thing, if the exponent of the fractional, here is a true root, as a^(n/m) = m√a^n.

Is the advice useful?