How to find the diagonal of an isosceles trapezoid

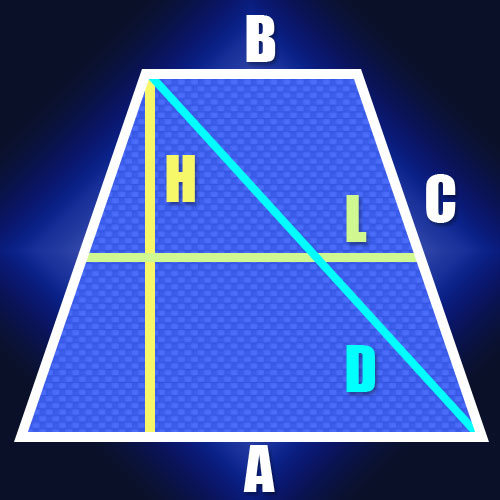
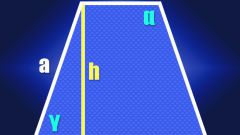
If you know the lengths of the bases of an isosceles trapezoid (A and B) and the length of its sides (C), to determine the lengths of the diagonals (D) we can use the fact that the sum of the squares of the lengths of all sides equals the sum of the squares of the lengths of the diagonals. This property stems from the fact that each of the diagonals of a trapezoid is the hypotenuse of a triangle, the legs of which serve as sidewall and the base. And according to Pythagoras the sum of the squares of the lengths of the legs is equal to the squared length of the hypotenuse. As the sides in an isosceles trapezoid are equal and its diagonals, then this property can be written in the form: A2 + B2 + 2C2 = 2D2. From this formula it follows that the length of the diagonal is equal to the square root of half the sum of the squares of the lengths of the bases, folded with the square of the length of the sides: D = √((A2 + B2)/2 + C2).

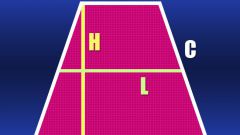
If the lengths of the sides is not known, but is the length of the middle line (L) and height (H) of an isosceles trapezoid, the length of the diagonal (D) is also easy to calculate. Since the length of the middle line is equal to the sum of the bases of the trapezoid, it gives us the opportunity to find the length of a line between a point on a larger basis, which lowered the height, and the top adjacent to the ground. In an isosceles trapezoid the length of this segment will coincide with the length of the middle line. Since the diagonal closes this segment and the height of the trapezoid into a right triangle, calculate its length is not difficult. For example, according to the same Pythagorean theorem it is equal to the square root of the sum of the squares of the height and the middle line: D=√(L2 + H2).

If you know the lengths of both bases of an isosceles trapezoid (A and B) and its height (H), then, as in the previous case, we can calculate the length of a line between point lowered on the big side elevation and the adjacent top. The formula from the previous step transformirovalsya like the following: D=√((A + B)2/4 + H2).